Question

An innocent boy was sitting on a perfectly hemispherical boulder of radius `R`. It was a dark and rainy night... He slides off the boulder while asleep (assume no friction). At what angle from the vertical, and at what height would he slide off?

Answer 1

What you can imagine is that there will be an evolving right triangle as the distance from the center vertical axis of the circle increases (this sketch's angles should not be considered to-scale).

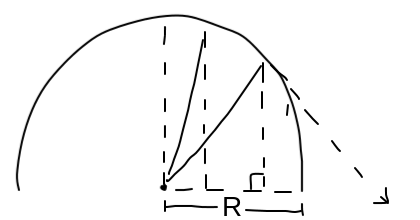
First, you should recognize that this is uniform circular motion caused by gravity. If we draw the free-body diagram for this, since there is no friction, there is no normal force. Thus, the only force acting is the force due to gravity. The sum of the forces should be the centripetal "force" (which isn't really a force).

You accelerate due to the contribution of the force due to gravity in the horizontal direction until you reach a max velocity, and then you fall off tangentially.

At this point, the force due to gravity only has a vertical component. So, one equation you can write down is:

`sum F = F_(g,y) = cancel(m)gcostheta_f = ma_c = (cancel(m)v_max^2)/R`

`color(green)(Rgcostheta_f = v_max^2)`

where `theta_f` is the fall angle from the vertical.

Therefore, what we want to know is when this maximum velocity is reached.

We don't get any other information, so now's a good time to consider kinetic and gravitational potential energies. Kinetic energy increases as you slide down, and potential energy decreases as your current height decreases. So, assuming `v_i = 0`:

`0 = DeltaK - DeltaU = (1/2mv_f^2 - cancel(1/2 mv_i^2)) - (mgDeltay)`

In terms of the original variables, we know that the angle with the vertical increases as you slide down, so the vertical distance `Deltay` ultimately traveled is `Rcostheta_i - Rcostheta_f`, where `theta_i = 0`:

`1/2cancel(m)v_f^2 = cancel(m)g(R - Rcostheta_f)`

`color(green)(v_max^2) = v_f^2 = color(green)(2gR(1 - costheta_f))`

Finally, let's substitute this back into the first equation:

`cancel(R)cancel(g)costheta_f = 2cancel(g)cancel(R)(1 - costheta_f)`

`costheta_f = 2 - 2costheta_f`

`color(blue)(theta_f = arccos(2/3))`

So that's the angle from the vertical at which the boy falls off... finally, we just need the fall height `h`, so we can use this angle (`~~48.2^@`) from the vertical to find the height.

`h = Rcostheta_f = color(blue)((2R)/3)`