Question

What is the difference between nodal surfaces and nodal planes?

Answer 1

A nodal surface is also called a radial node, which is a hollow spherical region in which electrons cannot be. A nodal plane is also called an angular node, which is either a plane where electrons cannot be, or a conic surface (`d_(z^2)` orbital).

---

Radial nodes (or nodal surfaces) can be found using the principal quantum number `n` and the angular momentum quantum number `l`, using the formula `\mathbf(n - l - 1)`.

• `n` goes as `1, 2, 3, . . . , N` where `N` is an integer, and `n` tells you the energy level.

• `l` goes as `0, 1, 2, . . . , n-1`, and `l` tells you the shape of the orbital. `l` is `0` for an `s` orbital, `1` for a `p` orbital, `2` for a `d` orbital, etc.

For instance, for a `1s` orbital:

• `l = 0`
• `n - l - 1 = 1 - 0 - 1 = \mathbf(0)` radial nodes.

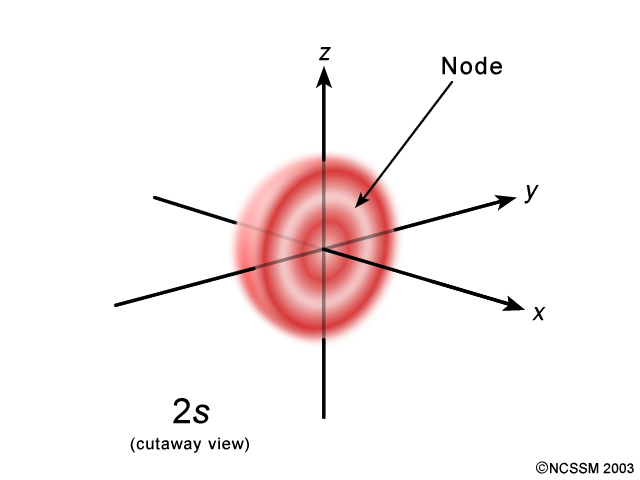
For a `2s` orbital:

• `l = 0` again
• `n - l - 1 = 2 - 0 - 1 = \mathbf(1)` radial node.

We can see the single radial node here as a white hollow sphere's cross-section:

Angular nodes (or nodal planes) can be found simply by determining `l`. For a `2p` orbital, `l = 1`, so there is `\mathbf(1)` angular node. However, `n - l - 1 = 2 - 1 - 1 = 0`, so it has `\mathbf(0)` radial nodes.

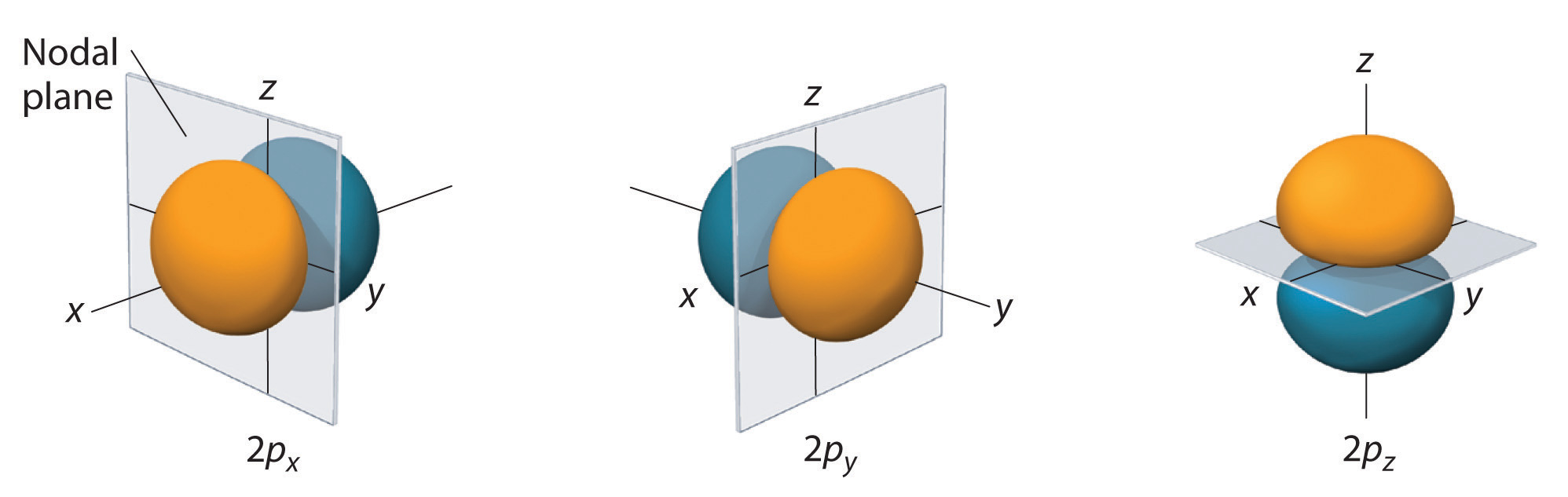
On the other hand, a `3p` orbital is distinctly different in that although it has `\mathbf(1)` angular node, it actually also has `\mathbf(1)` radial node; `n - l - 1 = 3 - 1 - 1 = 1`. We can see the radial node create a spherical "pocket" in the upper and lower lobes.