What is an example of a orbital probability patterns practice problem?
1 Answer
It's a bit of a difficult subject, but there are indeed some practical and not overly hard questions one could ask.
Suppose you have the radial density distribution (may also be known as "orbital probability pattern") of the
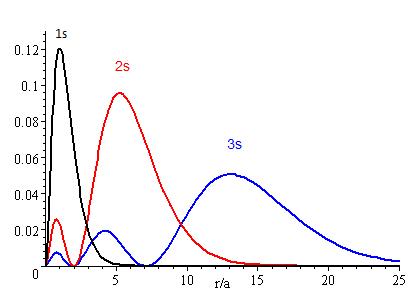
where
So one could ask some of the following questions:
- At what distances away from the center of each orbital should you expect to never find an electron?
- Why does the graph of the
#3s# orbital taper off farthest away from the center of the orbital, in comparison to the#1s# orbital, which tapers off closest to the center of the orbital (don't overthink it)?
Challenge question:
- Sketch an approximate probability distribution for each orbital listed above, knowing that a higher value on the y-axis indicates a darker shading for the orbital and vice versa, that
#r# indicates some distance outwards in all directions, and that#s# orbitals are spheres. It doesn't have to be super detailed; literally, draw dots.
(A probability distribution for an orbital is a distribution of points that indicate locations in the orbital where you can find an electron most often, least often, and anywhere in between.)
If you want to know the answer to the challenge question after you've tried it, here it is.

