Question #7f640
1 Answer
Here's what I got.
Explanation:
Ethanoic acid, also known as acetic acid,
The balanced chemical equation for this equilibrium reaction looks like this
#"CH"_3"COOH"_text((aq]) + "H"_2"O"_text((l]) rightleftharpoons "H"_3"O"_text((aq])^(+) + "CH"_3"COO"_text((aq])^(-)#
The equilibrium constant,
#K_(eq) = ( ["H"_3"O"^(+)] * ["CH"_3"COO"^(-)])/(["CH"_3"COOH"] * ["H"_2"O"])#
Since the concentration of water is presumed constant, you can rewrite this expression to get
#overbrace(K_(eq) * ["H"_2"O"])^(color(purple)(K_a)) = ( ["H"_3"O"^(+)] * ["CH"_3"COO"^(-)])/(["CH"_3"COOH"])#
This will give you the expression for the acid dissociation constant,
#color(green)(K_a = ( ["H"_3"O"^(+)] * ["CH"_3"COO"^(-)])/(["CH"_3"COOH"]))#
When acetic acid is titrated with a strong base, the neutralization reaction that takes place produces water and acetate ions, the conjugate base of the weak acid.
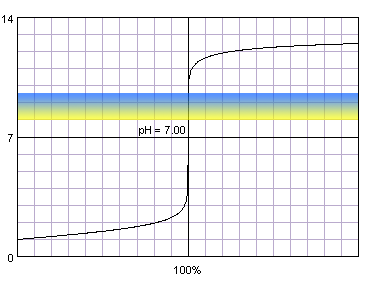
Right from the start, this tells you that the pH at equivalence point will be greater than
The balanced chemical equation for this reaction looks like this - I'll use hydroxide anions to represent sodium hydroxide
#"CH"_3"COOH"_text((aq]) + "OH"_text((aq])^(-) -> "CH"_3"COO"_text((aq])^(-) + "H"_2"O"_text((l])#
All the chemical species that are taking part in the reaction are found in a
Use the molarity and volume of the acid solution to find how many moles of acetic acid it containes
#color(blue)(c = n/V implies n = c * V)#
#n = "0.220 mol" color(red)(cancel(color(black)("dm"^(-3)))) * 25.0 * 10^(-3)color(red)(cancel(color(black)("dm"^(3)))) = "0.00550 moles CH"_3"COOH"#
In order to completely neutralize the acid, you need to add an equal number of moles of sodium hydroxide. Use the molarity of the sodium hydroxide solution to find what volume would contain this many moles
#color(blue)(c = n/V implies V = n/c)#
#V = (0.00550color(red)(cancel(color(black)("moles"))))/(0.150 color(red)(cancel(color(black)("mol"))) "dm"^(-3)) = "0.03667 dm"^3#
Rounded to three sig figs and expressed in cubic centimeters, the answer will be
#V_(NaOH) = color(green)("36.7 cm"^3)#
Because a complete neutralization leaves you with the acetate ion, a weak base, present in solution, the pH at equivalence point will be higher than
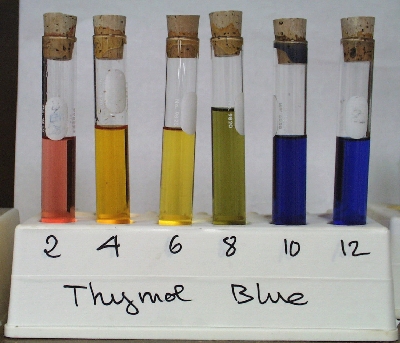
This means that you need an indicator that would change color at
As a final note, you said that
...I found its pH as 5.4...
If this is the value you have for the pH of the acid solution, you're calculations are incorrect.
I won't go in to that here, but using an ICE table will get you
#K_a = x^2/(0.220 - x)#
Here
#0.220 - x ~~ 0.220#
The concentration of hydronium ions will be
#x = sqrt(0.220 * K_a)#
#x = sqrt(0.220 * 1.74 * 10^(-5)) = 1.9565 * 10^(-3)"M"#
This will give you a pH of
#"pH" = - log(1.9565 * 10^(-3)) = color(green)(2.71)#