For the Hydrogen atomic #2s# wave function given by #psi = 1/(2sqrt(2pi)) sqrt(1/a_0) (2 - r/a_0)e^(-r//2a_0)#, at what radial distance away from the nucleus can no electrons be found?
2 Answers
Explanation:
The key to this problem lies with what characterizes a radial node.
Basically, the wave function,
The wave function that describes an electron in an atom is actually a product between the radial wave function, which is of interest in your case, and the angular wave function.
The radial wave function depends only on the distance from the nucleus,
Now, a node occurs when a wave function changes signs, i.e. when its passes through zero. A radial node occurs when a radial wave function passes through zero.
The important thing to remember about nodes is that an electron has zero probability of being located at a node. The probability of an electron being located at a particular point is given by the square of the absolute value of the wave function,
Since you have zero probability of locating an electron at a node, you can say that you have
#color(blue)(|Psi(x)|^2 = 0) -># this is true at nodes
So, you are given the wave function of a 2s-orbital
#Psi_(2s) = 1/(2sqrt(2pi)) * sqrt(1/a_0) * (2 - r/a_0) * e^(-r/(2a_0))#
and told that at
#|Psi_(2s)|^2 = 0#
Now, take a look at the wave function again. The only way to get the square of its absolute value equal to zero is if you have
#(2 - r/a_0) = 0#
since
#Psi_(2s) = overbrace(1/(2sqrt(2pi)) * sqrt(1/a_0))^(color(purple)(>0)) * (2 - r/a_0) * overbrace(e^(-r/(2a_0)))^(color(purple)(>0))#
This means that you have
#2 - r/a_0 = 0 implies r = 2 * a_0#
At
#color(green)(r_0 = 2 * a_0)#
Here's how the wave function for the 2s-orbital looks like
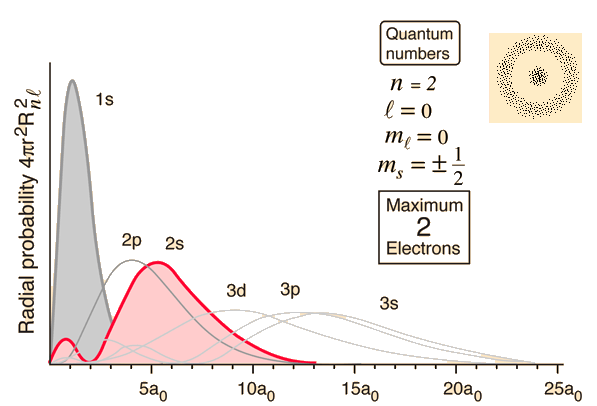
A 2s-orbital is characterized by the fact that it has no directional properties - you get the exact same value for its wave function regardless of the value of
This is why the 2s-orbital is spherical in shape.
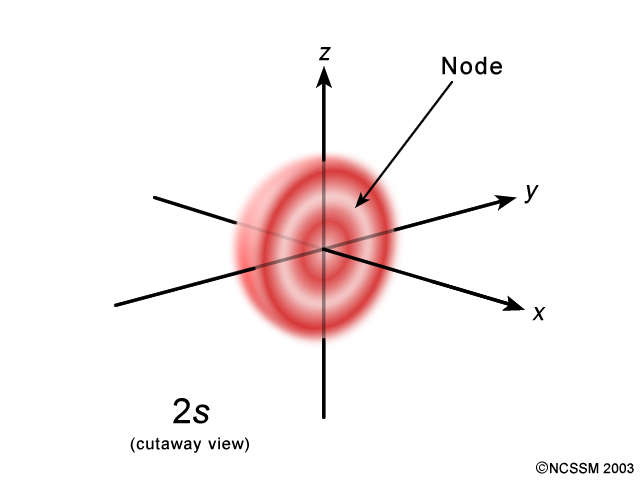
Moreover, this tells you that the wave function changes signs at the same distance from the nucleus in all directions, which is why a nodal surface is formed.
The wave function of a 2s-orbital changes signs once, so you only have one nodal surface here.
Here's an alternate approach.
Since the wave function shown has no time variable, let us define
SEPARATION OF VARIABLES GIVES RADIAL AND ANGULAR COMPONENTS
From the wave function you gave, you are showing
#psi(r,theta,phi) = R_(nl)(r)Y_l^(m_l)(theta,phi)#
#\mathbf(psi_(2s)(r,theta,phi) = R_(20)(r)Y_0^(0)(theta,phi))#
Now, the radial component in general is (Inorganic Chemistry, Miessler):
#color(green)(R_(20)(r) = 2(Z/(2a_0))^"3/2"(2-(Zr)/a_0)e^(-Zr"/"2a_0))#
And the angular component in general is
You can also tell that if you substitute in
NODES ARE FOUND WHEN THE PROBABILITY DENSITY IS 0
Now, you have a node wherever
#psi^"*"psi# (for real numbers,#psi^2# ), the probability density, as a whole is#0# .
For real numbers,
On the radial distribution graph for
However,
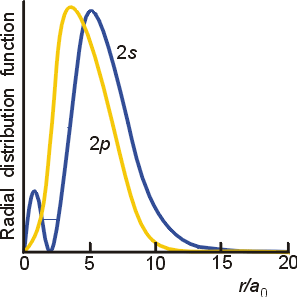
Since
Just from looking at the graph, we should see it close to
#0 = cancel(2)^(ne 0)cancel((Z/(2a_0))^"3/2")^(ne 0)(2-(Zr)/a_0)cancel(e^(-Zr"/"2a_0))^(>0)#
#color(green)(Zr = 2a_0)#
Now, since we are talking about the hydrogen atom,
We would know that that is the only one because the total number of radial nodes is


