Question #fb4b5
1 Answer
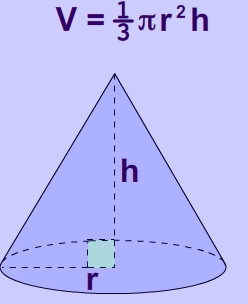
Yes, you use the formula for a cone volume to find the capacity.
depth =
capacity
Explanation:
Diameter
From the semicircular piece of metal we first find the circumference of the base of the cone, which is the same as ½ of the full circle,
Now find our cone radius from the cone circumference.
From Pythagoras, the equation for a right triangle