 )
)
To solve this problem is to resolve the initial velocity into its #x# and #y# components. As both the components are orthogonal to each other so these can be treated independently. Remember that horizontal time of flight is equal to the vertical time of flight.
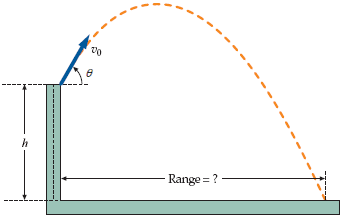
Let #h# be the height of the cliff.
Given is # angle theta=30^@, v_0=10.0m//s# and Range #100.0m#
(b) Lets find time of flight #t# to start with.
#x# component of initial velocity #=v_0cos theta=10.0xx cos 30 ^@#
#10.0xx0.8660=8.66m//s#
Time of flight #t=text{Range}/("Velocity in the "x " direction")#
or #t=100/8.66=11.547 s#
(c) #y# component of final velocity of ball just before the impact is given by the expression
#v=u+g t#,
taking value of acceleration due to gravity #g=9.81ms^-2#
Now the #y# component of initial velocity #v_0sin theta=10.0xxsin theta# #=10.0xx0.5=5.0m//s#.
As the gravity is acting in a direction opposite to the direction of motion, the ball rises up, comes to a stop and starts its descent downwards.
#v_y=5.0-9.81xx11.547=-108.276m//s#, #-ve # sign shows that it is in the #-y# direction.
If we ignore air resistance there will not be any change in the velocity in the #x# direction
Hence #v_f=sqrt(8.66^2+108.276^2)=108.6m//s# rounded to first place of decimal.
If #theta_f# is the angle made by the final velocity with the #y# axis at the time of impact, then
#tan theta_f=5/108.276#
or #theta_f=tan^-1 (5/108.276)approx 2.64^@# with the vertical
(a) The #y# component of initial velocity #=5.0m//s#.
When the ball is thrown up it has kinetic energy. Consider only #y# component of its velocity. As the ball rises, this kinetic energy gets converted in to potential energy relative to the top of cliff. At the highest point of flight, kinetic energy is zero and potential energy is maximum.
Once the ball reaches at a level equal to the top of cliff in its downward journey, #y# component of its velocity will be same as what it was at the time when it was thrown upwards but now it will be in the downwards direction. This is a consequence of Law of conservation of energy.
- Time taken to reach the maximum height
#v=u+g t#
#0=5-9.81t_1#
#=> t_1=9.81/5s#
- Time taken by the ball from the maximum height to the level of cliff back is same as #=t_1#
- Total time in this journey #2t_1=2xx9.81/5=1.019 s#
- Time taken from the level of cliff to the point of impact #=11.547-1.019=10.528s#
Now height of cliff #h=ut+1/2g t^2#. Consider the cliff's level
#h=5.0xx10.528+1/2xx9.81xx 10.528^2=596.3m# rounded to second place of decimal
 )
) 