Question #33a3c
2 Answers
Well.
Explanation:
There is only a downward force and no upward force so we will focus there.
Now, you are asked to find the velocity after t = 2 s and you know that the intial v is 0 since the box started from rest. You are going to have to use 1 of you kinematic equations
How do you find acceleration? Well you have found the net downward Force so using Newton's 2nd law of motion
Explanation:
Question
A 9.00-kg box sits on a ramp that is inclined at 33.00 above the horizontal. The coefficient of friction between the box and the surface of the ramp is 0.300. A constant horizontal force F = 26.0 N is applied to the box (as in Figure given below) , and the box moves down the ramp.If the box is initially at rest, what is its speed 2.00 s after the force is applied?
````````````````````````````````````````````````````````````````````````````````````````````````````````````````
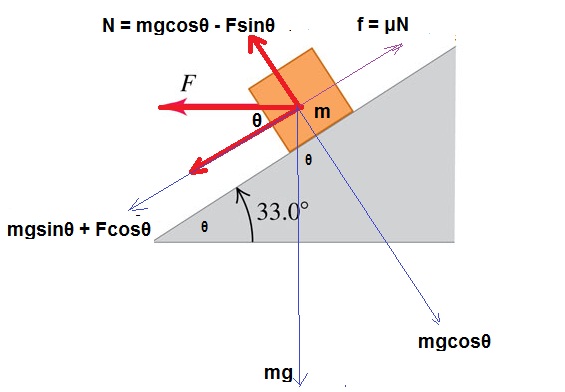
Answer
It is clear from the figure that the vertical component of applied force
So
Inserting
Now calculation of velocity 2s after the application of force F


