Why can only two electrons occupy each orbital?
2 Answers
- Electrons are "fermions", that means in any system can't be two of them having the same set of quantum numbers. The two electrons in the same orbital have two different spin quantum numbers
#m_s# and the same magnetic (#m_l# ), secondary (#l# ) and principal (#n# ) quantum numbers which are characteristic of the orbital. - The quantum numbers
#n# ,#l# ,#m_l# are "naturally" determined by - or necessary for - the process of solution of Schrödinger equation, under the constraint of yielding admissible wave functions. In particular the#m_l# quantum number, ranging in#2l+1# integers from#-l# to#+l# , determines the number of orbitals with the same#m_l# . This number is just one for#s# orbitals, because these spherical orbitals have#l=0# , that makes#m_l=0# the only possible magnetic quantum number. If#l=1# (that is possible only if#n>=2# ), you have a#p# orbital, and then there are three possible values for#m_l# :#-1, 0, +1# , which correspond to the three possible spatial directions#x, y, z# for the three#p# orbitals. With#l=2# (#n>=3# ), there are five admissible values of#m_l# :#-2, -1, 0, +1, +2# , corresponding to the five#d# orbitals, and so on.
Explanation:
About the first point
If an atom has
To put a third electron in the same orbital where there are already two electrons, is to put in the atom an electron with a duplicate set of quantum numbers, and that would violate the Pauli's exclusion principle.
About the second point
The Schrödinger equation is a sort of wave equation, whose solutions are waves (i.e. functions to describe the shapes of matter waves). To understand what does mean to find admissible wave functions, we can imagine to calculate, i.e. search for possible waveforms for a guitar string. Then, the only meaningful solutions are those which:
a) have zero amplitude in the end fixed points
b) are stationary (not changing in time)
c) the stationary distribution of amplitudes is symmetric and finite
So, the solution of the Schrödinger wave equation for the guitar string would yield these waves as possible solutions:
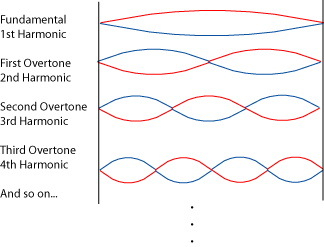
Here we have just one quantum number,
Passing to the three dimensions we gain two more quantum numbers with the following relations:
with
one
with
one
three
with
one
three
five
with
one
three
five
seven
... and so on.
The central reasons are the properties of fermions and the Pauli Exclusion Principle that follows.
The four quantum numbers are as follows:
-
#n# is the principal quantum number, which tells you the quantized energy level, and#n# takes on integer values in#{0, 1, 2, . . . , N}# . -
#l# is the angular momentum quantum number, which tells you the shape of the orbital (that is, whether it is an#s"/"p"/"d"/"f"/"g# orbital), and it takes on the values#{0, 1, 2, . . . , n-1}# . Each orbital subshell, e.g.#s, p, d, f, g# , corresponds to a particular#l# , i.e.#l = 0 -> s, l = 1 -> p, l = 2 -> d# , etc. -
#m_l# is the magnetic quantum number, which can also be called the vector projection of#l# . In the end, it basically corresponds to a unique possible orbital orientation (e.g.#p_x# ,#p_y# ,#p_z# for#l = 1# , which are all orthogonal to each other) in a subshell defined by#l# , and#m_l# takes on the values#{0, pm1, pm2, . . . , pml}# . That is, there are#2l+1# values for#m_l# , ranging from#-l# to#+l# in integer increments. -
#m_s# is the spin quantum number, and it tells you whether it's spin-up (#+"1/2"# for an electron) or spin-down (#-"1/2"# for an electron).
FERMIONIC BEHAVIOR
A fermion is a quantum mechanical particle that is antisymmetric with respect to the interchange of two of them. The important thing to us is that all fermions follow the Pauli Exclusion Principle, which says:
...two identical fermions (particles with half-integer spin) cannot occupy the same quantum state simultaneously.
An electron is an example of a fermion; it is a quantum mechanical particle that has half-integer spins. That is, it can have
Thus, electrons must also follow the Pauli Exclusion Principle.
WHY TWO ELECTRONS MAXIMUM PER ORBITAL?
Two electrons in the same orbital automatically have the same
For all real numbers,
That implies that for any two electrons in the same orbital,
So, there can only be a maximum of two electrons in a single orbital.
WHY A SPECIFIC NUMBER OF ORBITALS IN EACH SUBSHELL?
If we define
- For the same
#ns# orbitals, we have defined the same#n# , and we know that#l = 0# , so there can be#N_(m_l) = \mathbf(1)# orbitals in any#ns# subshell, and#N_(m_l)*N_(m_s) = 1*2 = \mathbf(2)# electrons in any#ns# subshell. - For the same
#np# orbitals, we have defined the same#n# , and we know that#l = 1# , so there can be#N_(m_l) = 2l+1 = \mathbf(3)# orbitals in any#np# subshell, and#N_(m_l)*N_(m_s) = (2l+1)*2 = 3*2 = \mathbf(6)# electrons in any#np# subshell. - For the same
#nd# orbitals, we have defined the same#n# , and we know that#l = 2# , so there can be#N_(m_l) = 2l+1 = \mathbf(5)# orbitals in any#nd# subshell, and#N_(m_l)*N_(m_s) = (2l+1)*2 = 5*2 = \mathbf(10)# electrons in any#nd# subshell.
and so on. That means we've established the following pattern:
#ns# subshells have one orbital and maximum two electrons.#np# subshells have three orbitals and maximum six electrons.#nd# subshells have five orbitals and maximum ten electrons.
and so on.


