Question

Question #f473f

Answer 1

Here's what I got.

Explanation:

As you know, four quantum numbers are used to describe the position and spin of an electron in an atom.

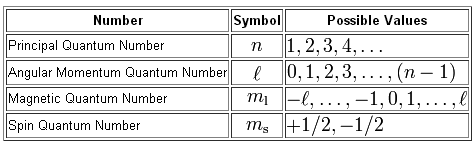
A good starting point here will be chlorine's electron configuration, which looks like this - I'll use the noble gas shorthand notation

`"Cl: " ["Ne"] 3s^2 color(red)(3)p^5`

As you can see, chlorine's outermost electrons are located in its 3p-subshell. Four of these five electrons are located in the `3p_z` and `3p_y` orbitals, and one electron is located in the `p_z` orbital.

Let's try to write a quantum number set for the electron located in the `p_z` orbital.

The principal quantum number, `n`, tells you the energy level on which the electron is located. In chlorine's case, this electron is located on the third energy level, `n = color(red)(3)`.

The angular momentum quantum number, which gives you the subshell in which the electron is located, takes values that range from `0` to `n-1`. More specifically, you have

• `l=0 ->` the s-subshell
• `l=1 ->` the p-subshell
• `l=2 ->` the d-subshell
  `vdots`

In your case, the electron is located in the p-subshell, you know that you have `l=1`.

The magnetic quantum number, `m_l`, gives you the exact orbital in which you can find the electron. For a p-subshell, the magnetic quantum number can be

• `m_l = -1 ->` the `p_x` orbital
• `m_l = color(white)(-)0 ->` the `p_y` orbital
• `m_l = color(white)(-)1 ->` the `p_z` orbital

Since we';re looking for the magnetic quantum number of an electron located in the `3p_z` orbital, you can say that you have `m_l = 1`.

Finally, the spin quantum number, which gives you the spin of the electron, can only have two possible values

`m_s = =1/2" "` or `" "m_s = -1/2`

Since the electron occupies the orbital by itself, you can attribute to it a spin magnetic number of `m_s = +1/2`.

This means that the quantum number set that describes the position and spin of the electron located in chlorine's `3p_z` orbital will be

`color(green)(|bar(ul(color(white)(a/a)color(black)(n = 3, l = 1, m_l = 1, m_s = +1/2)color(white)(a/a)|)))`