When the volume _______ at constant ________ the density increases?
1 Answer
Here is an alternative answer, which emphasizes that despite the "Fill-in-the-blank" nature of the question, there are two answers.
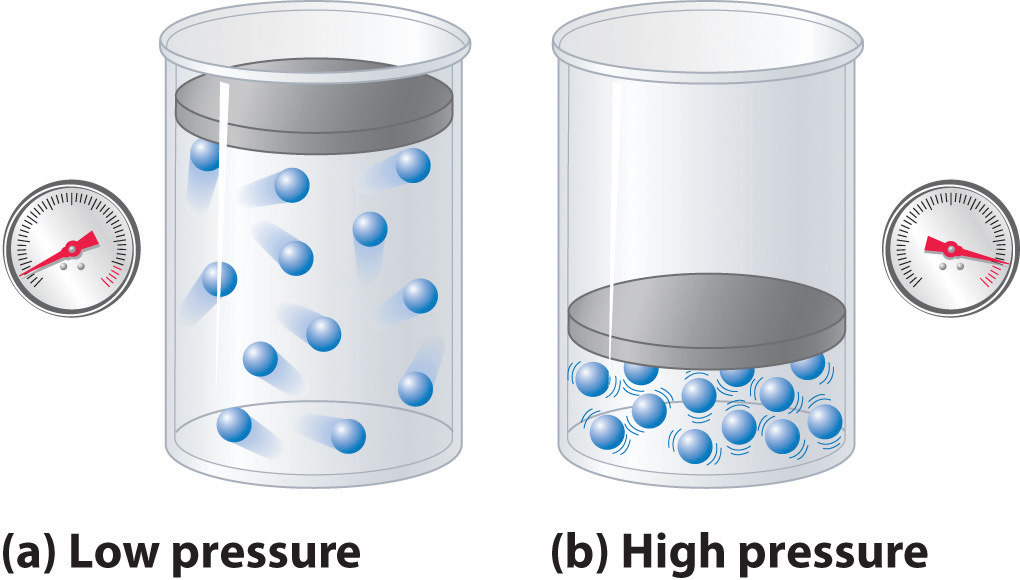
By definition, compression will involve decreasing the volume, hence moving gas particles closer together.
PRESSURE DEPENDENCE
Since pressure is proportional to the density of the gas distribution, and since density is defined as
ρ=mV ,where:
m is the mass in, say, grams.V is the volume, in, say, liters.then since the volume decreased, the density increased.
Alternatively, using the ideal gas law:
PV=nRT where
P is pressure,V is volume,n is themol s of gas (a measurable quantity),R is the universal gas constant (such as8.314472 J/mol⋅K ), andT is the temperature inK (∘C+273.15=K ).
When
 http://2012books.lardbucket.org/
http://2012books.lardbucket.org/
It does not, however, imply that for a real gas, a doubling of volume automatically implies a halving of pressure.
(That is why you will assume or have already assumed constant temperature on some ideal gas problems involving pressure and volume).
TEMPERATURE DEPENDENCE
Since some of the compression decreases the distance between each gas, it increases the likelihood of potential collisions, but decreases the "wiggle room" between gas particles. Each collision would transfer some kinetic energy between gas particles, but not a lot of it can be used since the particles can't move around as much.
So, the kinetic energy is constantly redistributed into the potential energy of the still gas particles (as per conservation of energy, energy is neither created nor destroyed, but redistributed).
(That is,

Since more gas particles have greater potential energy, it follows that the average kinetic energy has decreased, and consequently, since that is the definition of the temperature, the temperature has decreased as well.
This can be mathematically proven via the ideal gas law as before:
PV=nRT
When

