Question #b100e
1 Answer
Explanation:
For starters, I will assume that the problem meant
...note that the gas had double the volume when she started...
Now, Jessica's in luck because she can use Boyle's Law to find the initial pressure of the gas.
The idea here is that the temperature and number of moles of gas are being kept constant in the experiment, which means that you can use the direct relationship that exists between pressure and volume described by Boyle's Law.
Simply put, when temperature and number of moles of gas are being kept constant, increasing the pressure of the gas will result in a decrease in volume.
Likewise, decreasing the pressure of the gas swill result in an increase in volume.
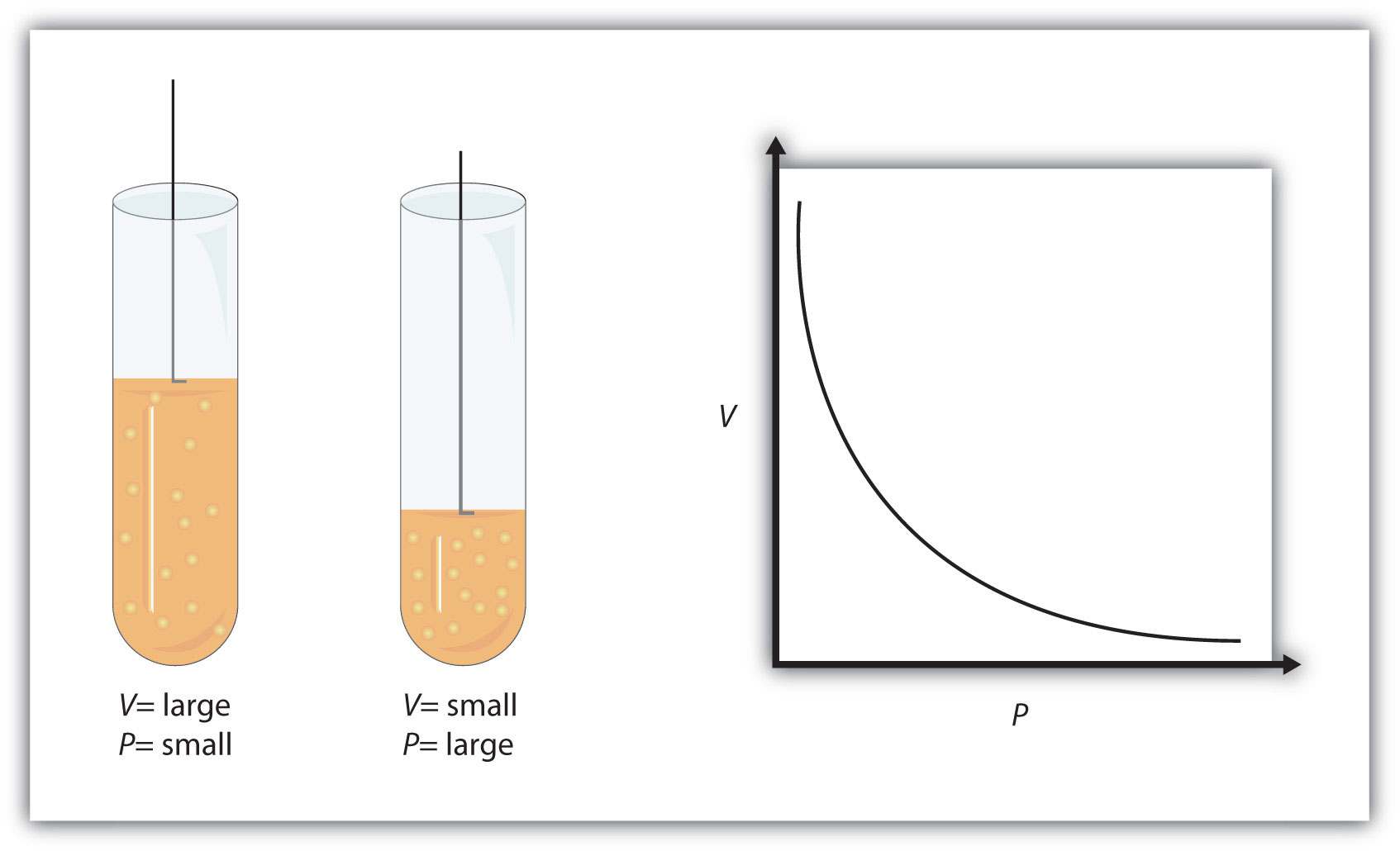
Now, Jessica knows that the gas had double the volume before the experiment started, which means that the volume of the gas got halved.
If you take
#V_2 = 1/2 * V_1" " " "color(orange)("(*)") -># the volume of the gas got halved
Mathematically, Boyle's Law can be expressed like this
#color(blue)(|bar(ul(color(white)(a/a)P_1V_1 = P_2V_2color(white)(a/a)|)))" "# , where
Your job here is to solve for
#P_1V_1 = P_2V_2 implies P_1 = V_2/V_1 * P_2#
Use equation
#P_1 = (1/2 * color(red)(cancel(color(black)(V_1))))/color(red)(cancel(color(black)(V_1))) * "300. kPa" = 1/2 * "300. kPa" = color(green)(|bar(ul(color(white)(a/a)"150. kPa"color(white)(a/a)|)))#
Now, does this result make sense?
According to Boyle's Law, a decrease in volume is the result of an increase in pressure. It thus follows that doubling the pressure of the gas would cause the volume to be halved.

