Question #c83bc
1 Answer
Explanation:
Since it's obvious that the question was mistyped, I will use the values given to you to show how volume decreases as a result of an increase in pressure.
You don't need to convert torr to atm because both the initial and the final pressure are expressed in atm.
The problem doesn't mention the temperature and number of moles of gas, which means that you can assume that they are being kept constant, When that is the case, pressure and volume have an inverse relationship described by Boyle's Law.
Simply put, when pressure increases, volume decreases, and when pressure decreases, volume increases.
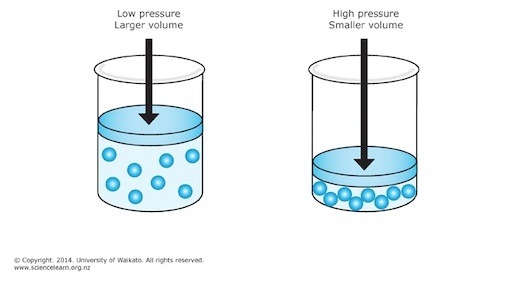
In your case, pressure increases from
Mathematically, Boyle's Law can be expressed as
#color(blue)(|bar(ul(color(white)(a/a)P_1V_1 = P_2V_2color(white)(a/a)|)))" "# , where
Rearrange to solve for
#P_1V_1 = P_2V_2 implies V_2 = P_1/P_2 * V_1#
Plug in your values to get
#V_2 = (2.5 color(red)(cancel(color(black)("atm"))))/(4.50color(red)(cancel(color(black)("atm")))) * "2 L" = color(green)(|bar(ul(color(white)(a/a)"1.1 L"color(white)(a/a)|)))#
I'll leave the answer rounded to two sig figs, despite the fact that you only have one sig fig for the initial volume of the gas.
As predicted, the volume decreased as a result of the increase in pressure.

