Question #d3743
1 Answer
A good estimate is
Explanation:
In order to predict what the density of 0calcium,
- the fact that atomic mass increases as you go down a group
- the fact that atomic radius also decreases as you go down a group
Calcium, strontium,
So, an element's density is affected by the mass of each individual atom and by the way these atoms are packed.
As you know, atomic mass Increases as you go down a group because elements get increasingly heavier nuclei. A quick look in a periodic table will show you that there are
This means that you can estimate that the difference in atomic mass will be the roughly same between calcium and strontium, and between strontium and barium.
Now, they key thing to keep in mind here is that atomic radius increases a bit more from calcium to strontium than it does from strontium to barium.
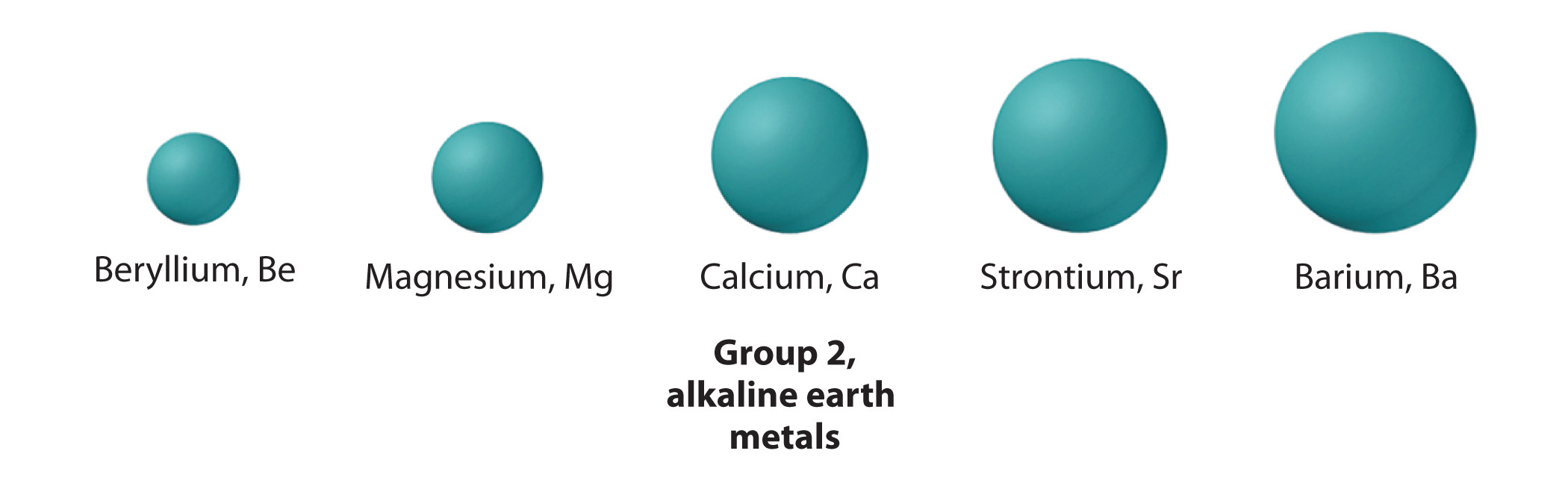
This happens because as you go down a group, electron shells are being added further and further away from the nucleus. However, the distance between these individual shells decreases as you move up in energy level.
This means that strontium's atomic radius is actually closer to that of barium than it is to that of calcium.
As a result, you should expect the density of strontium to be a little closer to that of barium that to that of calcium.
Calculate the change in density that occurs between strontium and barium
#Deltarho = |rho_"Sr" - rho_"Ba"|#
#Deltarho = | "2.62 g cm"^(-3) - "3.65 g cm"^(-3)| = "1.03 g cm"^(-3)#
If the changes in atomic mass and atomic radius were identical for all three elements, you would have said that the increase in density from calcium to strontium is equal to the increase in density between strontium and calcium
#Deltarho = |rho_"ca" - rho_"Sr"|#
This means that you would have
#rho_"Ca" = rho_"Sr" - Deltarho#
#rho_"Ca" = "2.62 g cm"^(-3) - "1.03 g cm"^(-3) = "1.59 g cm"^(-3)#
But since the change in density is a bit more significant when going from calcium to strontium than it is when going from strontium to barium, you can say that
#color(green)(|bar(ul(color(white)(a/a)color(black)(rho_"Ca" < "1.59 g cm"^(-3))color(white)(a/a)|)))#
This turns out to be a good estimate because the actual density of calcium is listed as
#rho_"Ca" = "1.55 g cm"^(-3)#

