Question

A circular medallion is to be electroplated with gold by using an electrolyte of `sf(Au_((aq))^(3+))`. Given the data below, how long will it take to plate a layer of gold `sf(1mum)` thick?

Diameter = 4 cm. Thickness = 2 mm. Density of gold = `sf(19.3"g/cm"^3)`.
`sf(F=9.6485color(white)(x)"C/""mol")`.
Current = 89 A.

Answer 1

`0.88color(white)(x)"s"`

Explanation:

Firstly I will find the volume of the plated medallion. Then subtract the volume of the unplated disc.

This will give me the total volume of gold. Given the density I can then get the mass of gold.

Since we know it is `Au^(3+)` I can find the quantity of charge needed to discharge this mass of gold.

Since current is the rate of flow of charge I can get the time taken to discharge this amount.

The first thing to do is put the lengths into a consistent unit as three different ones are used in the question. Since density is in `"g/cm"^(3)` I will put everything into `"cm"`.

Imagine a cross section like this:

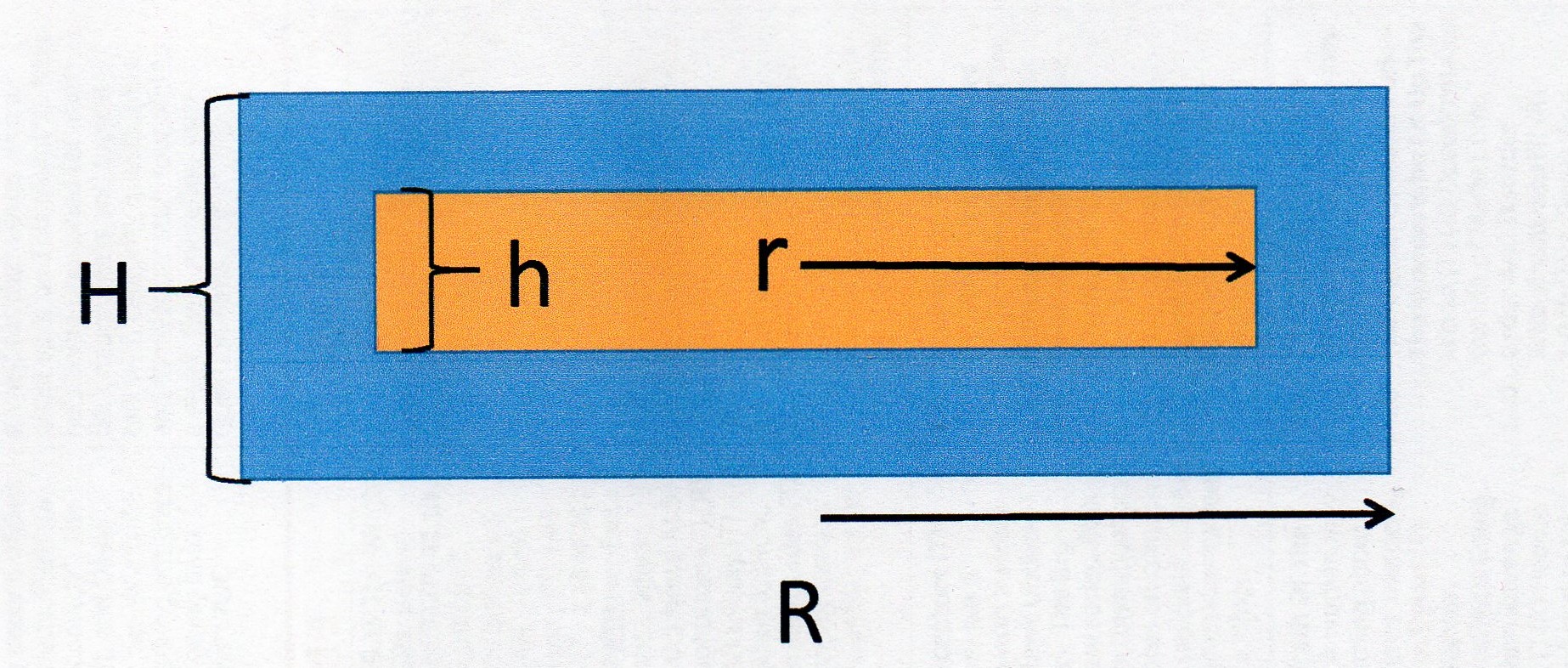
The blue area is the gold. The orange area is the medallion.

The volume of the plated disc `V` is given by:

`V=piR^(2)H`

The thickness of the layer is `1mum=10^(-6)m=10^(-4)cm`

So `R=(4/2 + 10^(-4))=2.0001cm`

The medallion is `2mm` thick. `1mm=0.1cm:.h=0.2cm`

`:.H=(0.2+2xx0.0001)=0.2002cm`

So the volume of the plated disc becomes:

`V=pi(2.0001)^(2)xx0.2002" "cm^(3)`

`V=pi(0.800880082)" "cm^(3)" "color(red)((1))`

The volume of the medallion `v` is given by:

`v=pir^(2)h`

`v=pi[2^(2)xx0.2]=pi(0.8)" "cm^3" "color(red)((2))`

To get the volume of gold in blue we subtract `color(red)((2))` from `color(red)((1))rArr`

`V_(Au)=pi[0.800880082-0.8] " "cm^(3)`

`V_(Au)=pi0.000880082" "cm^(3)`

`:.V_(Au)=0.00276486" "cm^(3)`

The density `rho` is given by:

`rho=m_(Au)/V_(Au)`

`:.m_(Au)=rhoxxV_(Au)=19.3xx0.00276486=0.0533618"g"`

The electrode equation is:

`Au^(3+)+3erarrAu`

This tells us that 1 mole of `Au` will require 3 moles of electrons to discharge.

The charge on 3 moles of electrons = `3xxF` where `F` is the charge on a mole of electrons and is the Faraday Constant which is `9.6485xx10^(4)"C/mol".`

The `A_r` of `Au` is `196.96657`

`:.196.99657"g"` require `3xx9.6485xx10^(4)=28.945xx10^(4)"C"`

`:.1"g"` requires `(28.945xx10^(4))/(196.99657)"C"`

`:.0.0533618"g"` require `(28.945xx10^(4))/(196.99657)xx0.0533618"C"`

`=78.405"C"`

Electric current `I` is the rate of flow of charge:

`I=Q/t`

`:.t=Q/I=78.405/89 "s"`

`t=0.881"s"`

In reality a current of `89"A"` is way too high. As well as being highly dangerous it would not give a good deposit. For a good finish you need a low current density (I/A).

Otherwise you get a spongy deposit which falls away easily.