Question #958e1
2 Answers
I tried this:
Explanation:
Well...to my limited knowledge (and because Stefan instigated me!) in a cyclotron, charged particles move in a vacuum chamber where there is a magnetic field perpendicular to the plane of the trajectories. In this configuration the charged particles are forced to describe a circular orbit of radius
Also, you have an electric field operated by an alternate generator applied to two hollow semi cylindrical electrodes with a space in betwen that accelerates continuously your particle horizontally (once in one and then to the other direction ).
So the magnetic field keeps your particle in a circular path and the variable electric field accelerate it!
Have a look:
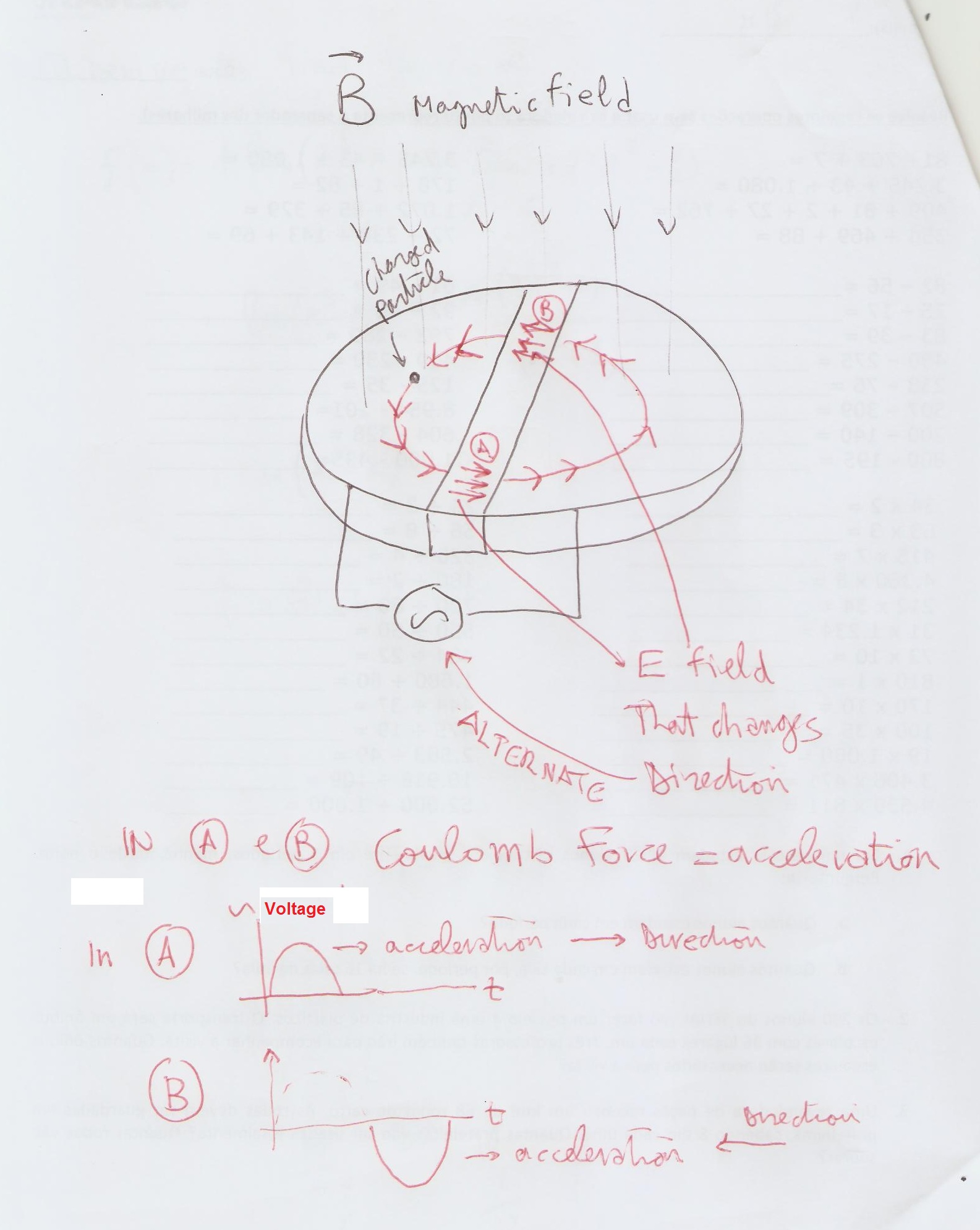
Hope I didn't confuse you even more!
Even though I am no expert as mentioned by Stefan, and also that Gio has already posted a beautiful answer, I feel obligated to write my answer. It goes as below.
Explanation:
Principle.
The operation of a cyclotron is based on the fact that the time period of the motion of a charged particle in a uniform magnetic field acting perpendicular to the direction of motion is independent of the velocity of the particle.
Lorentz's force equation for a charged particle moving in a combined electric and magnetic fields.
When a particle having charge
Considering the force due to orthogonal magnetic field to the velocity
The cross product is perpendicular to both the vectors. This provides turning force or centripetal force to the charge particle. If
Now Time period,
Or
inserting value of
or
or
The frequency
We observe that this is independent of both velocity of particle and also of radius of the circle in which particle moves.
The output energy, kinetic energy, of the particle can be found from (1)
We see that it is dependent on the strength of the magnetic field and radius in which the particle circles.
Practice.
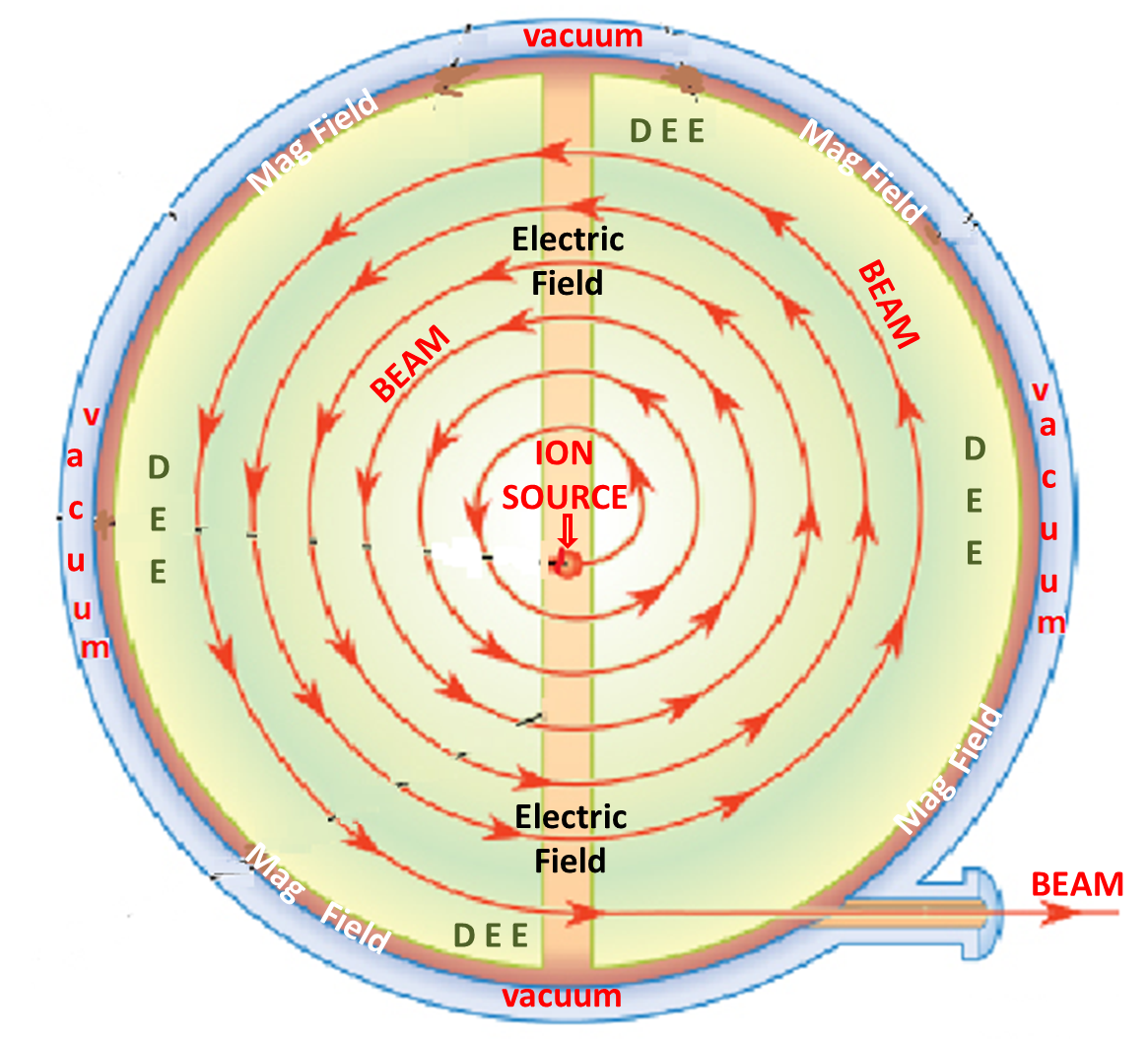
The construction of a cyclotron has been explained in the other answer posted by Gio.
Should you have any further queries, please feel free to raise.

