Question

Write the Hamiltonian for the lithium atom?

Answer 1

For the Schrodinger equation

`hatHpsi = Epsi,`

the wave function `psi` describes the state of a quantum-mechanical system such as an atom or molecule, while the eigenvalue of the Hamiltonian operator `hatH` corresponds to the observable energy `E`.

The energy consists of the components which describe:

• kinetic energy of each individual electron (`K_e`)
• kinetic energy of the nucleus (`K_n`). This is assumed zero based on the Born-Oppenheimer Approximation.
• instantaneous coulombic repulsion energy (two-particle interactions; `V_(ee)`). Also known as "interelectronic repulsion".
• nucleus-electron coulombic attraction energy (`V_(n e)`); really, it's a proton-electron attraction.
• nuclear repulsion energy (`V_(n n)`), assumed constant via the Born-Oppenheimer Approximation, which states that nuclear and electronic motion can be decoupled due to the large mass difference between nuclei and electrons. Hence, the nuclei are essentially stationary.

That means the Hamiltonian operator for an `N`-electron atom can be written in general as

`color(green)(hatH = hatK_e + cancel(hatK_n)^(~~0) + hatV_(ee) + hatV_(n e) + cancel(hatV_(n n))^("Assumed constant"))`

for each operator corresponding to the energy-component observables above. For lithium, we must use spherical harmonics (coordinates of `vecr,theta,phi`).

So, the Hamiltonian operator using atomic units for simplicity (relatively speaking...) is:

`color(green)(hatH) = stackrel(hatK_e)overbrace(\mathbf(-1/2[sum_(i=1)^(Z)1/(vecr_i^2)del/(delvecr_i)(vecr_i^2del/(delvecr_i)) - sum_(i=1)^(Z)(hatL_i^2)/(vecr_i^2)])) stackrel(hatV_(n e))overbrace(\mathbf(- sum_(i=1)^(Z) Z/(vecr_i))) stackrel(hatV_(e e))overbrace(\mathbf(+ sum_(i,j > i)^(Z)1/(vecr_(ij))))`

`= color(green)(-1/2[1/(vecr_1^2)del/(delvecr_1)(vecr_1^2del/(delvecr_1)) + 1/(vecr_2^2)del/(delvecr_2)(vecr_2^2del/(delvecr_2)) + 1/(vecr_3^2)del/(delvecr_1)(vecr_3^2del/(delvecr_3)) - (hatL_1^2)/(vecr_1^2) - (hatL_2^2)/(vecr_2^2) - (hatL_3^2)/(vecr_3^2)] - 3/(vecr_1) - 3/(vecr_2) - 3/(vecr_3) + 1/(|vecr_1 - vecr_2|) + 1/(|vecr_1 - vecr_3|) + 1/(|vecr_2 - vecr_3|))`

where:

• `hatL_i^2 = hatL_(ix)^2 + hatL_(iy)^2 + hatL_(iz)^2`

`= - (y_idel/(delz_i) - z_idel/(dely_i))^2 -(z_idel/(delx_i) - x_idel/(delz_i))^2 - (x_idel/(dely_i) - y_idel/(delx_i))^2`

is the square of the angular momentum operator for electron `i`. This is what contains the `theta` and `phi` components.

• `vecr_i` is the radial distance between electron `i` and the nucleus.
• `vecr_(ij)` is the radial distance between electron `i` and electron `j`, where `\mathbf(i ne j)`.
• `del/(delvecr_i)` is the partial derivative with respect to the radial distance of electron `i` from the nucleus.
• `Z` is the atomic number.
• The atomic units simplified `-h^2/(8pi^2m)` as `-1/2` for the coefficient of the kinetic energy operator.
• The atomic units simplified `-(Ze)/(4piepsilon_0vecr_i)` as `-Z/(vecr_i)` for the nucleus-electron coulombic attraction.
• The atomic units simplified `(e^2)/(4piepsilon_0vecr_(ij))` as `1/(vecr_(ij))` for the interelectronic repulsion.

That's the short version, anyway. The full version (still in atomic units) is here:

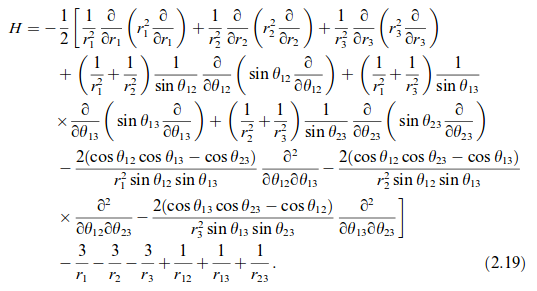
Ignoring interelectronic repulsions for hydrogen-like lithium (`"Li"^(2+)`), we would have:

`color(blue)(hatH)`

`~~ color(blue)(-1/2[1/(vecr_1^2)del/(delvecr_1)(vecr_1^2del/(delvecr_1)) + 1/(vecr_2^2)del/(delvecr_2)(vecr_2^2del/(delvecr_2)) + 1/(vecr_3^2)del/(delvecr_1)(vecr_3^2del/(delvecr_3)) - (hatL_1^2)/(vecr_1^2) - (hatL_2^2)/(vecr_2^2) - (hatL_3^2)/(vecr_3^2)] - 3/(vecr_1) - 3/(vecr_2) - 3/(vecr_3))`

or if including the wave function operated on, it would be:

`color(blue)(hatHpsi)`

`= {\mathbf(-1/2[sum_(i=1)^(Z)1/(vecr_i^2)(del)/(delvecr_i)(vecr_i^2(del)/(delvecr_i)) - sum_(i=1)^(Z)(hatL_i^2)/(vecr_i^2)]) \mathbf(- sum_(i=1)^(Z) Z/(vecr_i)) \mathbf(+ sum_(i,j > i)^(Z)1/(vecr_(ij)))}\mathbf(psi)`

`= -1/2[sum_(i=1)^(Z)1/(vecr_i^2)(delpsi)/(delvecr_i)(vecr_i^2(delpsi)/(delvecr_i)) - sum_(i=1)^(Z)(hatL_i^2psi)/(vecr_i^2)] - sum_(i=1)^(Z) Z/(vecr_i)psi + sum_(i,j > i)^(Z)1/(vecr_(ij))psi`

`~~ color(blue)(-1/2[1/(vecr_1^2)(delpsi)/(delvecr_1)(vecr_1^2(delpsi)/(delvecr_1)) + 1/(vecr_2^2)(delpsi)/(delvecr_2)(vecr_2^2(delpsi)/(delvecr_2)) + 1/(vecr_3^2)(delpsi)/(delvecr_1)(vecr_3^2(delpsi)/(delvecr_3)) - (hatL_1^2psi)/(vecr_1^2) - (hatL_2^2psi)/(vecr_2^2) - (hatL_3^2psi)/(vecr_3^2)] - 3/(vecr_1)psi - 3/(vecr_2)psi - 3/(vecr_3)psi)`

---

The wave function... for obvious reasons, will be written as the short version.

`color(blue)(psi_(nlm_l)(vecr,theta,phi))`

`= psi_(nlm_l)(vecr_1, vecr_2, vecr_3,theta_(12), theta_(13), theta_(23))`

`= color(blue)(R_(nl)(vecr_1, vecr_2, vecr_3)Y_(l)^(m_l)(theta_(12),theta_(13),theta_(23)))`

where:

• `R_(nl)(vecr_i)` is the radial wave function for electron `i`.
• `Y_(l)^(m_l)(theta_(ij))` for `i ne j` is the angular wave function for the angular separation between electron `i` and electron `j`.
• `n`, `l`, and `m_l` are the typical quantum numbers.

You can find the full general `R_(nl)(vecr)` and `Y_(l)^(m_l)(theta,phi)` here.