Question #c62e7
3 Answers
The area is bounded by the maroon lines and the blue dots.
Explanation:
The area is bounded by the maroon lines and the blue dots.
So we can break down the region into 2 parts:
Note we are interested in the upper region so the area in each case is:
Explanation:
Referencing the picture in the other answer, we can split this into two integrals. The first is the region bounded on the interval
#int_-2^0(4-x^2)dx=[4x-x^3/3]_-2^0#
#=[4(0)-0^3/3]-[4(-2)-(-2)^3/3]#
#=0-[-8+8/3]#
#=16/3#
We have to add this value to the amount bounded by
The triangle has a height of
The area of
Here is a third way to find the answer to this question. Rotate your thinking
Explanation:
The region is shown below:
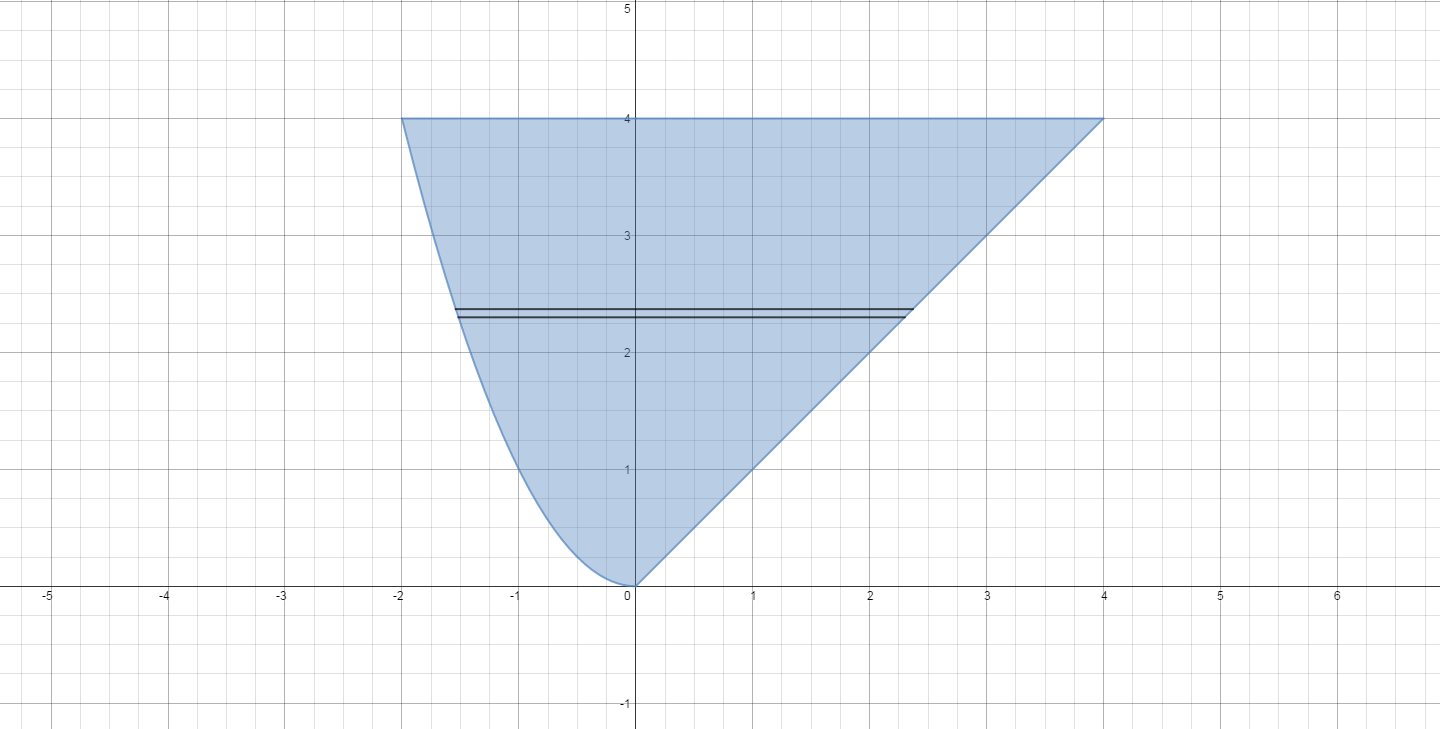
We can think of the region as the collection of points whose
Note that the left branch of
On the right it is easy to see that
Our method is analogous to finding an area between
we can integrate with respect to
Greater
"
# = y^2/2+2/3sqrty^3]_0^4#
# = 8 + 16/3 = 40/3#



