Question

Which of these is true for ideal gases?

Pressure and volume are directly proportional.
Pressure and mols are directly proportional.
Volume and temperature are inversely proportional.

Answer 1

Only the second one is true.

Explanation:

Let's start by writing down the ideal gas law equation, which looks like this

`color(blue)(|bar(ul(color(white)(a/a)PV = nRTcolor(white)(a/a)|)))" "`, where

`P` - the pressure of the gas
`V` - the volume it occupies
`n` - the number of moles of gas
`R` - the universal gas constant, usually given as `0.0821("atm" * "L")/("mol" * "K")`
`T` - the absolute temperature of the gas

---

1)

When temperature, `T`, and number of moles, `n`, are kept constant, the right-hand side of the ideal gas law equation is constant

`PV = overbrace(nRT)^(color(red)("constant")`

`PV = color(red)("constant")`

In order for pressure to be directly proportional to the volume of the gas when temperature and number of moles are kept constant, it must increase when volume increases or decrease when volume decreases.

As you can see from the above equation, the product `P xx V` is constant, which can only mean that when pressure increases, volume must decrease and when pressure decreases, volume must increase.

This means that under these conditions, pressure and volume have an inverse relationship known as Boyle's Law.

---

2)

Next, when temperature and volume are held constant, pressure is directly proportional to the number of moles of gas. This time, rearrange the ideal gas law equation to isolate the terms that are being kept constant on one side of the equation

`PV = nRT implies P/n = overbrace((RT)/V)^(color(red)("constant"))`

`P/n = color(red)("constant")`

This time, when the number of moles of gas increases, pressure must increase as well in order for that ratio to remain constant. Likewise, when the number of moles of gas decreases, pressure must decrease as well.

This means that under these conditions, pressure and number of moles of gas are directly proportional.

Does this make sense?

As you know, gas pressure is caused by the collisions between the gas molecules and the walls of the container. The stronger and more frequent these collisions are, the higher the pressure will be.

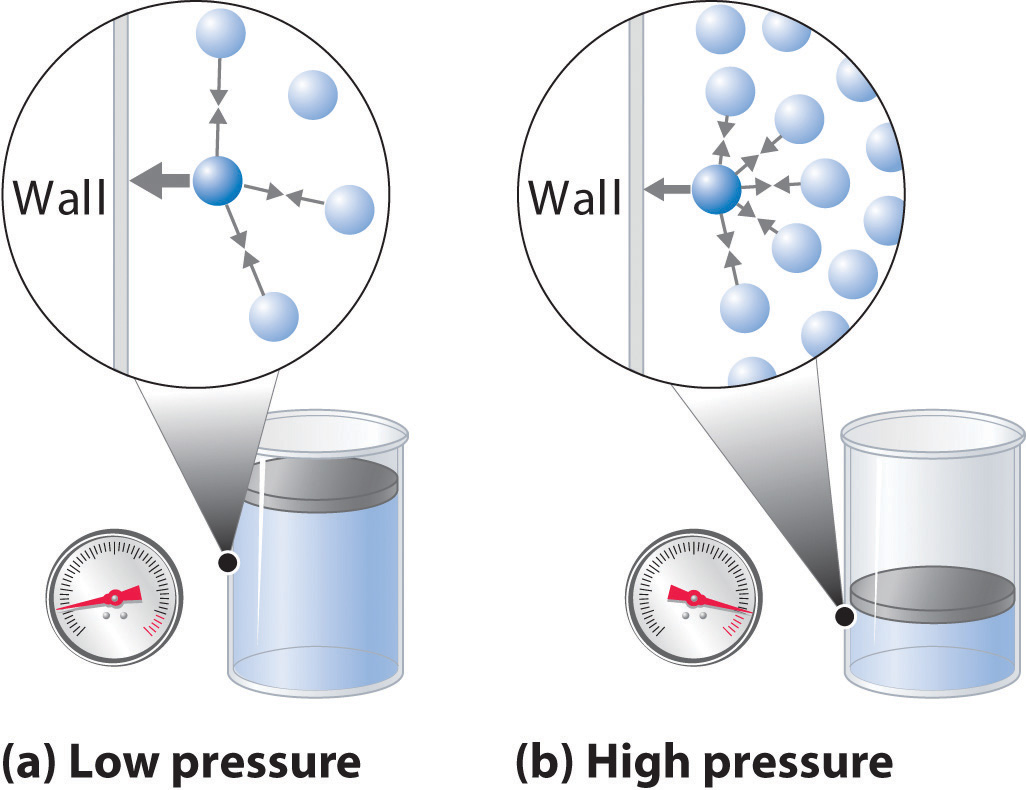
Increasing the number of moles of gas is equivalent to increasing the number of collisions between the molecules of gas and the walls of the container `->` pressure will increase as well.

---

3)

Finally, when pressure and number of moles of gas are kept constant, volume is directly proportional to temperature.

Rearrange the ideal gas law equation to find

`PV = nRT implies V/T = overbrace((nR)/P)^(color(red)("constant")`

`V/T = color(red)("constant")`

Once again, in order for that ratio to be constant, you need volume to increase when temperature increases and to decrease when temperature decreases.

Therefore, under these conditions, volume and temperature are directly proportional, not inversely proportional.