How do I calculate the average kinetic energy using the equipartition theorem?
1 Answer
DISCLAIMER: Kind of long answer, but the bottom half simply reconciles the discrepancy in the answer we get in the example.
The equipartition theorem (in the context of Physical Chemistry and Physics) is a way to assign degrees of freedom (DOFs) to a gas, assuming ideality, meaning that we assume each DOF equally contributes to the average energy.
A degree of freedom is simply a dimension in which the gas can move in the specified way. So...
- Since we evidently live in a 3-dimensional world, the translational DOFs total
#\mathbf(3)# :#x# ,#y# , and#z# . - The rotational DOFs total
#\mathbf(2)# for linear molecules (a third rotation axis would be the internuclear axis, which returns the same molecule back), or#\mathbf(3)# for nonlinear molecules (#x,y,z# rotational axes). - The number of vibrational modes available are
#\mathbf(3N - 5)# for linear polyatomic molecules or#\mathbf(3N - 6)# for nonlinear polyatomic molecules, where#N# is the number of atoms in the molecule, but#N = 1# maximum for vibrations. Note that these may include degenerate vibrations. - The electronic DOFs are generally considered negligible and so it's usually fine to omit them.
Perhaps a bit confusing, but the equipartition theorem as it relates to internal energy is often written as:
#\mathbf(stackrel("Molar Internal Energy")overbrace(barU) = N/2RT)# ,where:
#N# is the number of DOFs (not the number of atoms in the molecule... bad coincidence).#R# is the universal gas constant,#"8.314472 J/mol"cdot"K"# .#T# is the temperature at which you observe the gas, in#"K"# .
EXAMPLE (MOLAR CONSTANT-VOLUME HEAT CAPACITY)
So, for our example, let's say we looked at
According to the equipartition theorem, it has:
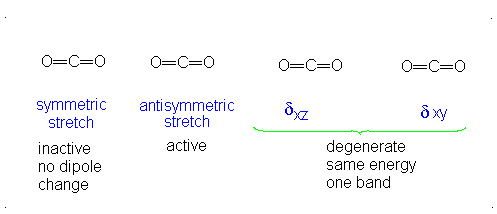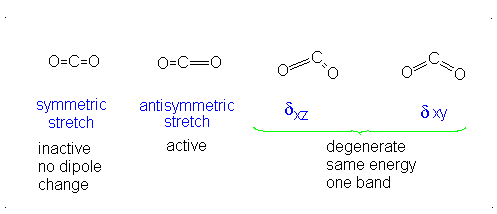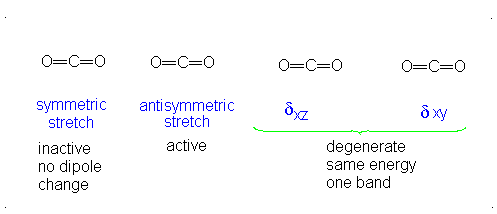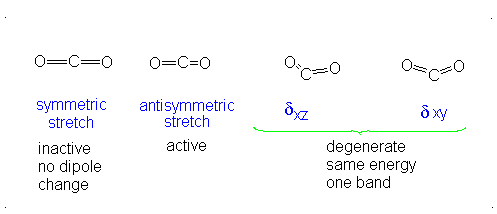
#3# translational DOFs#2# rotational DOFs#1# vibrational DOF (corresponding to#4# vibrational modes, i.e. stretching/bending motions) is presumed to be accounted or, but two are degenerate---same in energy.
Therefore,
#\mathbf(barC_V = barC_(V,"trans") + barC_(V,"rot") + barC_(V,"vib"))#
#~~ \mathbf(N/2R)# , where#R# is the universal gas constant.
#=> 3/2R + 2/2R + R = \mathbf(7/2R) ~~ color(green)("29.099 J/mol"cdot"K")# .
The actual
CAVEAT ABOUT EQUIPARTITION THEOREM ON POLYATOMIC MOLECULAR GASES
It's worth mentioning that the equipartition theorem is not particularly accurate on polyatomic molecular gases when it comes to their vibrational DOF.
It often overestimates on
To get
#\mathbf(barC_(V,"vib") = Rsum_(i = 1)^(3N - 5)[g_i((theta_i)/T)^2 e^(-theta_i"/"T)/(1-e^(-theta_i"/"T))^2])# where:
#g_i# is the degeneracy of vibrational mode#i# .#theta_i# is the characteristic vibrational temperature of vibrational mode#i# in#"K"# .- Other variables have been defined previously.
For nonlinear polyatomics, just replace
#3N - 5 = 4# .- The symmetric stretch (mode
#1# ) has#g_i = 1# . - The asymmetric stretch (mode
#2# ) has#g_i = 1# . - The bends have
#g_i = 2# . #theta_1 = "1890 K"# #theta_2 = "3360 K"# #theta_(3,4) = "954 K"# (doubly-degenerate)
So at
#barC_(V,"vib") = R[stackrel("Symmetric Stretch")overbrace(((("1890 K")/("298.15 K"))^2(e^(-1890"/"298.15)/(1-e^(-1890"/"298.15))^2))) + stackrel("Asymmetric Stretch")overbrace(((("3360 K")/("298.15 K"))^2(e^(-3360"/"298.15)/(1-e^(-3360"/"298.15))^2))) + stackrel("Two Degenerate Bends")overbrace(2*((("954 K")/("298.15 K"))^2(e^(-954"/"298.15)/(1-e^(-954"/"298.15))^2)))]#
Eventually, you should get
So, the corrected value of
#color(blue)(barC_V) = 3/2R + 2/2R + 0.9822R = 3.4822R#
#= color(blue)("28.953 J/mol"cdot"K")#
And indeed, even closer! (less than