Question #52e7f
1 Answer
- See explanation
Explanation:
Using the appropriate
#color(blue)"Addition Formulae"#
#color(red)(|bar(ul(color(white)(a/a)color(black)(cos(A±B)=cosAcosB∓sinAsinB)color(white)(a/a)|)))# hence cos(x-y)=cosxcosy+sinxsiny
We are given sinx and cosy but require to find cosx and siny to evaluate the right side of the expansion.
Using the following sketches (not to scale)
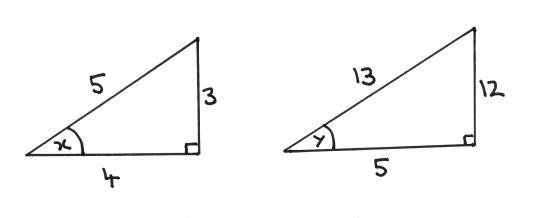
#sinx=3/5 "allows opposite and hypotenuse to be completed"# Use
#color(blue)"Pythagoras' theorem"# to find adjacent = 4 or recognise the well known '3,4,5' triangle.
#sinx=3/5rArrcosx=4/5#
#"------------------------------------------------------"# Similarly
#cosy=5/13# allows adjacent and hypotenuse to be completed. Using Pythagoras or recognising '5,12,13' triangle to obtain opposite = 12.
#cosy=5/13rArrsiny=12/13#
#"-----------------------------------------------------------"# We now have all the required ratios to complete the expansion.
#cos(x-y)=cosxcosy+sinxsiny#
#=(4/5xx5/13)+(3/5xx12/13)#
#=20/65+36/65=56/65" thus shown"#
