(i) My diagram looks like as below
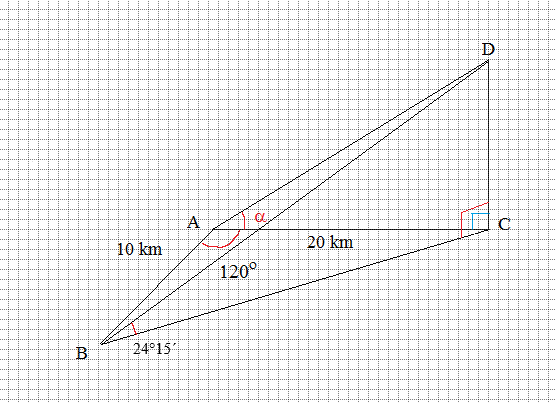
(ii) In #Delta ADC#, after converting all distances to meters.
#tan alpha=(CD)/20000#
#=>CD=2.0xx10^4tan alpha " meter"#
(iii) We make use of cosine rule.
For a triangle with sides #a,b and c# and angles #A, B and C# the cosine rule states:
#a^2 = b^2 + c^2 - 2bc cos A#
Applying in #DeltaABC# where #angle A=120^@#
#BC^2 = (2.0xx10^4)^2 + (1.0xx10^4)^2 - 2xx2.0xx10^4xx1.0xx10^4 cos 120^@#
We know that #cos120^@=-1/2#
#=>BC^2 = 4.0xx10^8 + 1.0xx10^8 + 2.0xx10^8#
#=>BC^2 = 7.0xx10^8 #
#=>BC = sqrt(7.0xx10^8) #
#=>BC = sqrt7xx10^4 " meter"#
(iv) In #DeltaBDC#
#tan25^@15'=(CD)/(BC)#
Making use of values found in (ii) and (iii)
#tan25^@15'=(2.0xx10^4tan alpha)/(sqrt7xx10^4)#
Solving for #alpha#
#tan alpha=sqrt7 /2tan25^@15'#
#alpha=tan^-1(0.6239)#
#alphaapprox32^@#, correct to nearest degree.
