Question #3419a
1 Answer
Jul 6, 2016
(a)
(b)
Explanation:
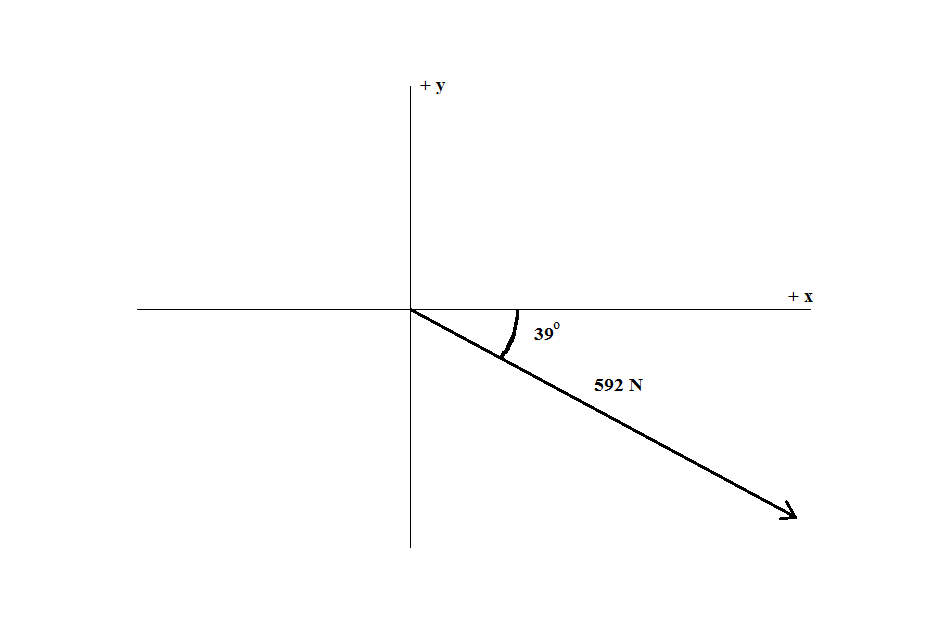
The figure above shown the position of the force vector whose
(a) the
Inserting value of
(b)
(
Inserting value of
(a)
(b)

The figure above shown the position of the force vector whose
(a) the
Inserting value of
(b)
(
Inserting value of