Question

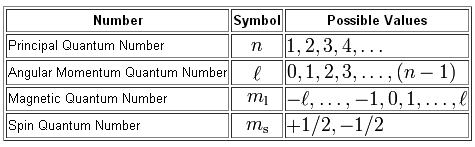
Question #f4b81

Answer 1

Seven electrons.

Explanation:

Your starting point here will the electron configuration of a neutral iron atom, `"Fe"`.

Iron is located in period 4, group 8 of the periodic table and has an atomic number equal to `26`. This means that the electron configuration of a neutral iron atom must account for a total of `26` electrons

`"Fe: " 1s^2 2s^2 2p^6 3s^2 3p^6 3d^6 4s^2`

Now, a set of four quantum numbers is assigned to each of those `26` electrons.

Your goal here is to figure out how many electrons have

`n + l + m_l = 4`

It's important to realize that for every set of `n`, `l`, and `m_l` quantum numbers that match your criteria, you get two electrons, one having spin-up, `m_s = +1/2`, and the other having spin-down, `m_s = -1/2`.

Starting with the electrons located on the first energy shell, `n=1`, you will have

`n= 1" " implies" " l = 0 " "implies " "m_l = 0`

The two electrons located on the first energy level can have only one set of `n`, `l`, and `m_l` numbers. The difference between the two electrons is made by the spin quantum number, `m_s = +- 1/2`.

For the electrons located on the second energy level, `n=2`, you will have

`n=2 " "implies" "{ (l=0 " "implies" "m_l = color(white)(-1) 0 color(white)( +1)), (l=1 " "implies" " m_l = {-1, 0, 1}) :}`

This time you can have

`n = 2, " "l = 1, " "m_l = +1 " "implies" " 2 + 1 + 1 = 4`

This set of `n`, `l`, and `m_l` quantum numbers belongs to two electrons located on the second energy shell, in the `color(blue)(2p_y)` orbital, one having spin-up and the other with spin-down.

For the electrons located on the third energy level, `n=3`, you will have

`n=3 " "implies" "{ (l=0 " "implies" "m_l = color(white)(-1) 0 color(white)( +1)), (l=1 " "implies" " m_l = {-1, 0, 1}), (l=2 " "implies" " m_l = {-2, -1, 0, +1, +2}) :}`

This time you can have

`n = 3, " " l=1, " "m_l = 0 " "implies" " 3 + 1 + 0 = 4`

This set of `n`, `l`, and `m_l` quantum numbers belongs to two electrons located on the third energy level, in the `color(purple)(3p_z)` orbital, one having spin-up and the other spin-down.

Notice that you can also have

`n=3, " " l=2, " " m_l = -1 " " implies" " 3 + 2 + (-1) = 4`

This set of `n`, `l`, and `m_l` quantum numbers belongs to one electron located on the third energy level, in the `color(brown)(3d_(yz))` orbital, having spin-up.

This is the case because iron has a total of `6` electrons in its 3d-subshell. This implies that only one of the five 3d-orbitals is completely filled, the other four being only half-filled.

`color(white)()`
`color(white)()`

`color(white)()`

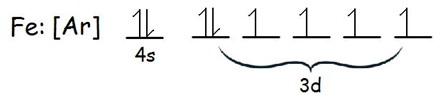
If you assign `m_l=-2` to the 3d-orbital that contains two electrons, let's say `3d_(xz)`, you will end up with a single electron in the orbital that corresponds to `m_l = -1`, which would be `color(brown)(3d_(yz)`, the one following the `3d_(xz)` orbital.

Finally, for the electrons located on the fourth energy level, `n=4`, you will have

`n=4 " "implies" "l=0 " "implies" "m_l = 0`

Notice that iron has only two electrons on its fourth energy level, both in the `color(red)(4s)` orbital, so you don't need to worry about other values of `l`.

These two electrons share the `n`, `l`, and `m_l` numbers for which

`n=4, " " l=0, " " m_l = 0 " "implies" " 4 + 0 + 0 = 4`

So, the total number of electrons for which

`n + l + m_l = 0`

is equal to

`"no. of e"^(-) = overbrace(color(white)(a)2color(white)(a))^(color(blue)("located in 2p"_ y)) + overbrace(color(white)(a)2color(white)(a))^(color(purple)("located in 3p"_ z)) + overbrace(color(white)(a)1color(white)(a))^(color(brown)("located in 3d"_ (yz))) + overbrace(color(white)(a)2color(white)(a))^(color(red)("located in 4s")) = color(green)(|bar(ul(color(white)(a/a)color(black)("7 e"^(-))color(white)(a/a)|)))`