First, we use the important identity #sin2theta=2sinthetacostheta#:
#sin2theta-costheta=0#
#->2sinthetacostheta-costheta=0#
Now we can factor out #costheta#:
#2sinthetacostheta-costheta=0#
#->costheta(2sintheta-1)=0#
And using the zero product property, we obtain solutions of:
#costheta=0" and "2sintheta-1=0->sintheta=1/2#
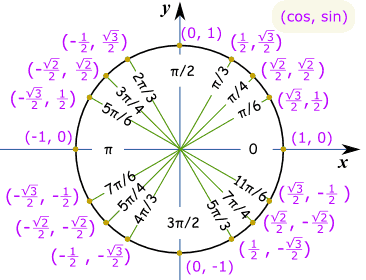
So, when does #costheta=0# on the interval #-pi/2<=theta<=(3pi)/2#? The solutions can be found by using the unit circle and a property of the cosine function:
#cos(-theta)=costheta#
If #theta=pi/2#, then:
#cos(-pi/2)=cos(pi/2)#
From the unit circle, we know that #cos(pi/2)=0#, which also means #cos(-pi/2)=0#; so two solutions are #-pi/2# and #pi/2#. Also, the unit circle tells us that #cos((3pi)/2)=0#, so we have another solution there.
Now, onto #sintheta=1/2#. Again, we will need the unit circle to find our solutions.
We know from the unit circle that #sin(pi/6)=1/2#, and #sin((5pi)/6)=1/2#, so we add #pi/6# and #(5pi)/6# to the list of solutions.
Finally, we put all of our solutions together: #theta=-pi/2, pi/6, pi/2, (5pi)/6#, and #(3pi)/2#.
The Unit Circle