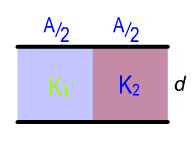
We have a case of a parallel-plate capacitor that has plate area #A# with a plate separation of #d# filled with dielectric strontium titanate up to half depth, similar to the figure as shown above. The remaining depth is empty and therefore has air as dielectric. It is clear that both dielectrics cover half the area#A/2# of the parallel plates.
Capacitance #C=(kepsilon_0A)/d# ......(1)
where #k# is relative permittivity of dieletric material, and #epsilon_0# is permittivity of free space #=8.854xx10^-12Fm^-1#
#k=1# for free space, #k>1# for all media and #kapprox1# for air.
Both dielectrics #k_1 ("air")and k_2("strontium titanate")# experience the same potential difference as both are connected to the same parallel plates on either sides. This is exactly the same situation as two capacitors connected in parallel where
Total capacitance #C_"total"=C_"air"+C_"dielectric"# .....(2)
Using (1) and information given above
#C_"total"=(epsilon_0A/2)/d+(kepsilon_0A/2)/d#
#=>C_"total"=(epsilon_0A)/(2d)(1+k)#
Taking the relative permittivity of strontium titanate as #310# we get
#C_"total"=(311epsilon_0A)/(2d)#
Inserting given values in SI units we get
#C_"total"=(311xx8.854xx10^-12xx200/10^4)/(2xx4/10^3)#
#=>C_"total"=6.88xx10^-9F#, rounded to two decimal places.

