A 330 pF capacitor and a 220 pF capacitor in series are each connected across a 6 V dc source. What is the voltage across the 330 pF capacitor?
1 Answer
Explanation:
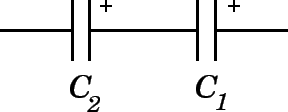
For capacitors in series like this the total charge stored by each capacitor is the same.
The capacitance
So:
Let
and
So:
The voltage drop across the 2 capacitors = 6V so we can write:
We have 2 simultaneous equations here so from
We can now substitute this expression for
- which is the voltage drop across the
#330"pF"# capacitor.
This also means that

