Question

Question #db592

Answer 1

Here's what I got.

Explanation:

Your starting point here is the electron configuration of a neutral atom of iron, `"Fe"`, which looks like this -- I'll use the noble gas shorthand notation

`"Fe: " ["Ar"] 3d^6 4s^2`

As you know, when an atom of iron forms a `2+` cation it loses two electrons from its highest-energy orbital.

It is very important to keep in mind that these two electrons will come from the `4s` orbital, which is actually higher in energy than the `3d` orbitals when occupied.

The iron(II) cation, `"Fe"^(2+)`, will have the following electron configuration

`"Fe"^(2+): ["Ar"] 3d^6`

So, you know that the two electrons that are being lost when iron forms the iron(II) cation are coming from the `4s` orbital.

A total of four quantum numbers can be used to describe the location and spin of an electron in an atom.

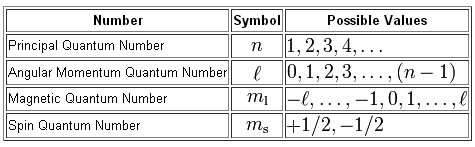
The principal quantum number, `n`, tells you the energy level on which an electron is located. In this case, both electrons are coming from a `4s` orbital, so you have

`n = 4 ->` the fourth energy level

The angular momentum quantum number, `l`, tells you the subshell in which the electrons reside. For electrons located on the fourth energy level, the angular momentum quantum number can take the following values

• `l=0 ->` the s-subshell
• `l=1 ->` the p-subshell
• `l=2 ->` the d-subshell
• `l=3 ->` the f-subshell

Your electrons are located in the `4s` subshell, so you have

`l = 0 ->` the s-subshell

The magnetic quantum number, `m_l`, tells you the exact orbital in which an electron is located, i.e. the orientation of the orbital.

The s-subshell can only hold one orbital, since

`l= 0" "` and `" "m_l = -l, ..., -1, 0, 1, ..., +l`

The two electrons will thus have

`m_l = 0 ->` the s-orbital

Finally, the spin quantum number, `m_s`, tells you the spin of the electron. This quantum number can take one of two possible values

• `m_s = -1/2 ->` an electron having spin-down
• `m_s = +1/2 ->` an electron having spin-up

In your case, both electrons are coming from the same orbital, which means that the ymust have opposite spins. You can thus say that the two electrons can be described by the following quantum sets

`color(green)(|bar(ul(color(white)(a/a)color(black)(n = 4, l=0, m_l = 0, m_s = -1/2)color(white)(a/a)|)))`

An electron located on the fourth energy level, in the `4s` subshell, in the `4s` orbital, having spin-down

`color(green)(|bar(ul(color(white)(a/a)color(black)(n = 4, l=0, m_l = 0, m_s = +1/2)color(white)(a/a)|)))`

An electron located on the fourth energy level, in the `4s` subshell, in the `4s` orbital, having spin-up