Question #45ff0
1 Answer
Here's what I got.
Explanation:
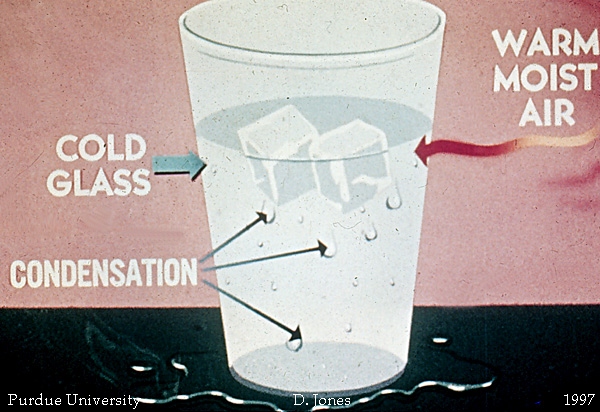
The idea here is that some of the water present in Petri dish will evaporate, which is why the system, which I assume is the water drop + Petri dish, is losing mass.
Now, some of the newly evaporated water will come into contact with the underside of the lid and condense on the surface of the lid, which is why the lid is gaining mass.
SIDE NOTE I don't think that all the water will evaporate and all the vapor will condense, but you can work with that assumption if it makes things easier to visualize.
The ice chip is placed on the top of the lid to decrease the temperature of the lid. Some of the ice melts as heat is being transferred from the lid to the ice cube, which is why you need to wipe the outside top of the lid.
You can thus say that you have
(A)
My assumption would be that only some of the liquid water initially placed in the Petri dish will evaporate as time elapses.
(B)
The fog that you observe on the underside of the lid is simply water vapor. Some of the water molecules present in the liquid state in the water drop will go into vapor state.
This is what happens when evaporation takes place.
(C)
The water in the system undergoes a liquid
#"H"_ 2 "O"_ ((l)) rightleftharpoons "H"_ 2"O"_ ((g))#
(D)
The mass of the lid changes because when some of the water molecules that are now present in the gaseous state come into contact with the cold surface of the lid, they condense to form liquid water
#"H"_ 2"O"_ ((g)) rightleftharpoons "H"_ 2"O"_ ((l))#
As a result, the mass of the lid will increase because it now has added water molecules on its underside.
On the other hand, the mass of the system must decrease because some of the water molecules have left the liquid state, which implies that the mass of water decreased as more and more water molecules evaporated.
(E)
If you assume that all of the molecules that evaporated from the drop of liquid water also condensed on the underside of the dish, then you must say that
#color(purple)(|bar(ul(color(white)(a/a)color(black)("mass lost by system " = " mass gained by the lid")color(white)(a/a)|)))#
This is what the Law of Mass Conservation is all about.
For example, if all the water evaporated and all the vapor condensed on the lid, the mass of the system would decrease by the mass of the drop of water and the mass of the lid would increase by the mass of the drop of water.
Now, let's assume that only some of the water evaporated and some of the vapor condensed. Let's say that the initial drop of water has a mass
Now, a mass
In this case, some of the evaporated water
#f * m - g * f * m = (1-g) * f * m#
will remain in the vapor state. You can thus say that the system lost more mass,
Remember that
#f * m > f * g * m#


