Are #csctheta^2# and #csc^2theta# same or different?

Question

1104 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-02-12T14:35:40

#csctheta^2# and #csc^2theta# are different. Please see below for details.

#csctheta^2# and #csc^2theta# are different.

Let us see the figure below.
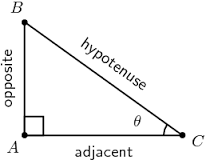
enter image source here
From the definition of trigonometric ratios, #csctheta=("hypotenuse")/("opposite side")#

and #csc^2theta=(csctheta)^2=cscthetaxxcsctheta#

= #("hypotenuse")^2/("opposite side")^2#

However, #csctheta^2# is the cosecant ratio of #theta^2#.

Now if #theta# is in degrees, #theta^2# does not work out.

Hence while considering #theta^2#, we consider it only in radians.

Now for example , if #theta=pi/3#

#csc^2theta=csc^2(pi/3)=(2/sqrt3)^2=4/9=0.4444#

For working out #csctheta^2#, we have

#theta=pi^2/9=9.8696/9=1.0966#

and using scientific calculator, with #theta=1.0966# in radians

#csctheta^2=csc1.0966=1.124#