The y-intercept will occur at #(0, 2)#:
#y = 1/3(0)^3 - 4(0) + 2 = 2#
The function's derivative can be found by the power rule, which states that #d/dx(x^n) = nx^(n - 1)#.
#y' = x^2 - 4#
The slope of the tangent is given by evaluating your point #x= a# into the derivative. The normal line is perpendicular to the tangent line, or the product of their two slopes equals #-1#.
The slope of the tangent is #m = 0^2 - 4 = 0 - 4 = -4#. Then the slope of the normal line is #1/4#.
Since the reaction passes through #(0, 2)#, the normal line has equation:
#y - y_1 = m(x - x_1)#
#y - 2 = 1/4(x - 0)#
#y - 2 = 1/4x#
#y = 1/4x + 2#
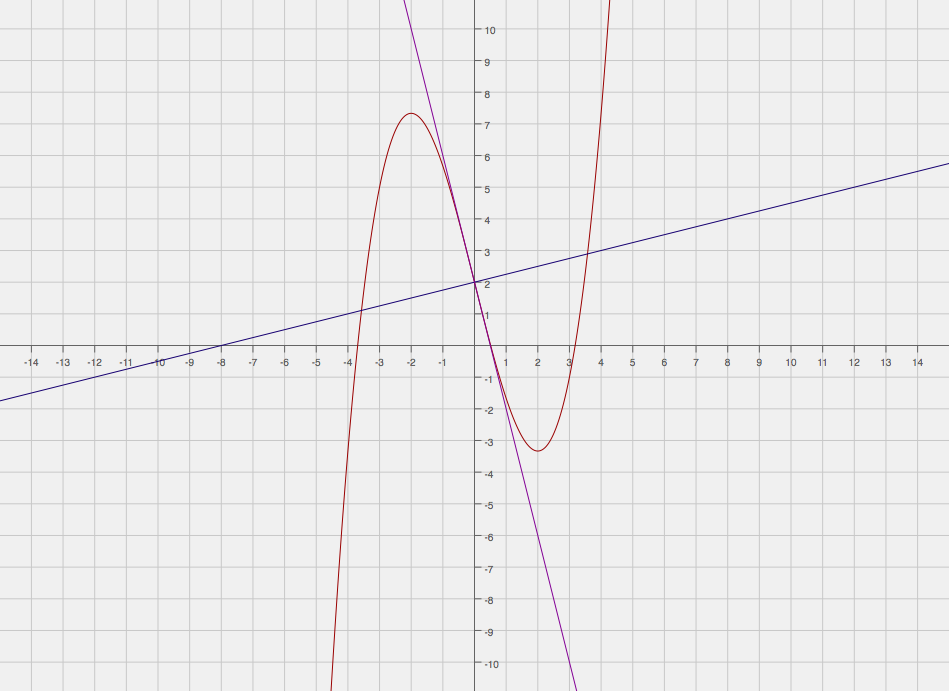
Here is a graphical depiction of the problem. The graph in #color(red)("red")# is the function #y = 1/3x^3 - 4x + 2#, the graph in #color(purple)("purple")# is the tangent line and the graph in #color(blue)("blue")# is the normal line.
Hopefully this helps!


