The terminal arm of angle #A# goes over the point #(1/5, -1/5)#. What is the exact value of #secA#?

Question

1964 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-11-08T14:23:12

#secA = sqrt(2)#

The definition of #secA# is #1/cosA = 1/("adjacent"/"hypotenuse") = "hypotenuse"/"adjacent"#.

Now consider the following diagram.

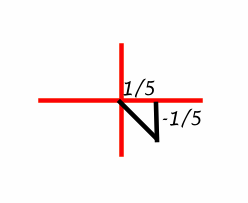
enter image source here

We know the point on the terminal arm, so we know the two legs of the imaginary triangle above. However, we need the hypotenuse to find #secA#.

#a^2 + b^2 = c^2#

#(1/5)^2 + (-1/5)^2 = c^2#

#1/25 + 1/25 = c^2#

#2/25 = c^2#

#c= sqrt(2)/5 -> "no negative solution since we're talking about the hypotenuse"#

We know that #secA = "hypotenuse"/"adjacent"#, so we have that :

#secA= (sqrt(2)/5)/(1/5)#

#secA = sqrt(2)#

Hopefully this helps!