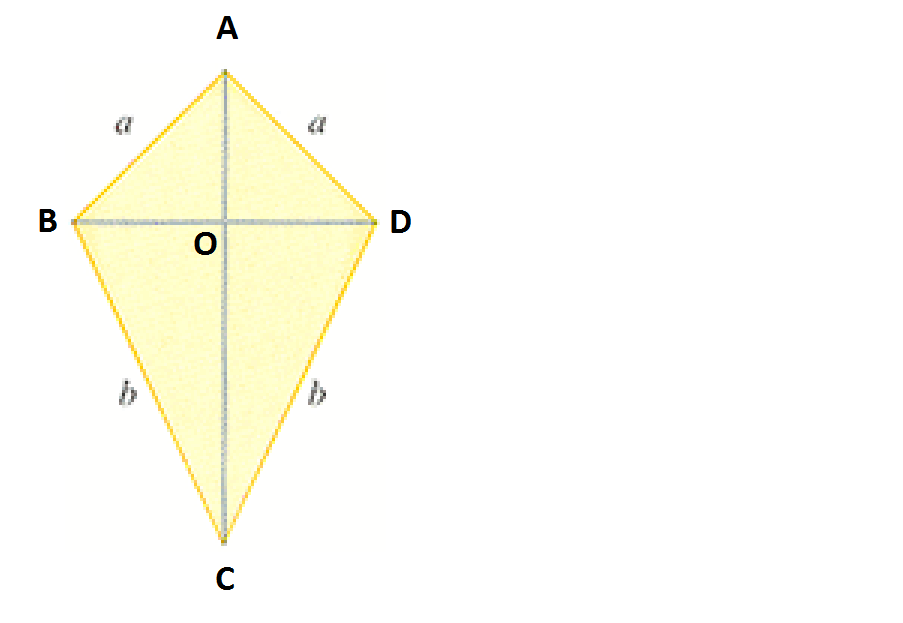
Label the vertices of the kite as above. Let #x_1 = BD# and #x_2=AC#, the lengths of the diagonals. Our goal is to find #x_1# and #x_2# such that the area of the kite #A = (x_1x_2)/2# is maximal.
First we will write #x_2# in terms of #x_1#, #a#, and #b#. Note that #OD = (BD)/2 = x_1/2#, #AD = a#, and #CD = b#.
Notice, before proceeding, that the triangle inequality applied to #triangleABD# gives #x_1 < 2a#, and applied to #triangleBCD# gives #x_1<2b#.
Applying the Pythagorean theorem to the right triangle #AOD#, we have #AO^2+OD^2=AD^2#
#=> AO^2 = AD^2-OD^2#
#=> AO = sqrt(AD^2-OD^2) = sqrt(a^2-(x_1/2)^2)#
Similarly, if we apply the Pythagorean theorem to the right triangle #COD#, we get #CO^2 + OD^2 = CD^2#
#=> OC^2 = CD^2-OD^2#
#=> OC = sqrt(CD^2-OD^2) = sqrt(b^2-(x_1/2)^2)#
Putting these together, we get #x_2# as
#x_2 = AC=AO+OC=sqrt(a^2-x_1^2/4)+sqrt(b^2-x_1^2/4)#
(Note that the restrictions on #x_1# mentioned above ensure that the arguments of the square roots are positive)
Next, we will find #x_1# such that #A=(x_1x_2)/2# is maximal.
Rewriting the area using the formula for #x_2# we found above, we get
#A = (x_1x_2)/2=1/2x_1(sqrt(a^2-x_1^2/4)+sqrt(b^2-x_1^2/4))#
To maximize this, we will find its extrema by locating its critical values, points where its derivative is #0# or does not exist. The differentiation process is lengthy and is omitted to save space, but can be done using the product rule and chain rule. Doing so, together with some algebraic manipulation, we find #(dA)/(dx_1)# to be
#((sqrt(4a^2-x_1^2)+sqrt(4b^2-x_1^2))(sqrt(4a^2-x_1^2)sqrt(4b^2-x_1^2)-x_1^2))/(4sqrt(4a^2-x_1^2)sqrt(4b^2-x_1^2))#
which is equal to #0# if and only if one of
#{(sqrt(4a^2-x_1^2)+sqrt(4b^2-x_1^2)=0), (sqrt(4a^2-x_1^2)sqrt(4b^2-x_1^2)-x_1^2=0):}#
are true.
The first equation has no solutions given our restrictions, as both terms are positive and the sum of two positives cannot be #0#. Solving the second:
#sqrt(4a^2-x_1^2)sqrt(4b^2-x_1^2) - x_1^2 = 0#
#=> sqrt(4a^2-x_1^2)sqrt(4b^2-x_1^2) = x_1^2#
#=> (4a^2-x_1^2)(4b^2-x_1^2) = x_1^4#
#=> x_1^4-4a^2x_1^2 - 4b^2x_1^2 + 16a^2b^2 = x_1^4#
#=> 4(a^2+b^2)x_1^2 = 16a^2b^2#
#=> x_1^2 = (4a^2b^2)/(a^2+b^2)#
As #x_1# is a length, it must be positive, so we only need consider the positive square root of #x_1^2#.
#:. x_1 = sqrt((4a^2b^2)/(a^2+b^2)) = (2ab)/sqrt(a^2+b^2)#.
And if we substitute our formula for #x_1^2# into our formula for #x_2#, we get
#x_2 = sqrt(a^2-(a^2b^2)/(a^2+b^2))+sqrt(b^2-(a^2b^2)/(a^2+b^2))#
#=sqrt((a^4+a^2b^2-a^2b^2)/(a^2+b^2))+sqrt((b^4+a^2b^2-a^2b^2)/(a^2+b^2))#
#=sqrt(a^4/(a^2+b^2))+sqrt(b^4/(a^2+b^2))#
#=(a^2+b^2)/sqrt(a^2+b^2)#
#=sqrt(a^2+b^2)#