Question #0d7b8
2 Answers
i) see below
ii) In the graph of an even function the left side relative to the Y-axis is a reflection of the right side (relative to the Y-axis),
Explanation:
i) using the identity:
ii) Note that the reflection of the right side of
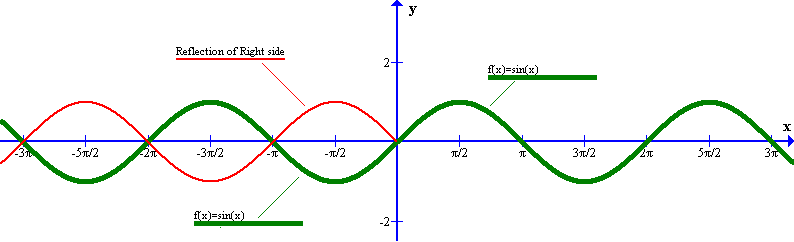
Therefore
and
When x is expressed in radian, the Maclaurin series for cos x and sin
x are
,
It follows that
If
So, sine is even and cosine is odd.
For even functions y = f(x), like cos x,
if (x, y) is on the graph, then (-x, y) is on
it. So, the graph is symmetrical about the y-axis.
For odd f like sin x,
if (x, y) is on the graph, so is (x, -y). And so, the graph is
symmetrical about x-axis.
