What is a conical node? How can you find one?
1 Answer
It's a kind of angular node that you can see, for instance, in the
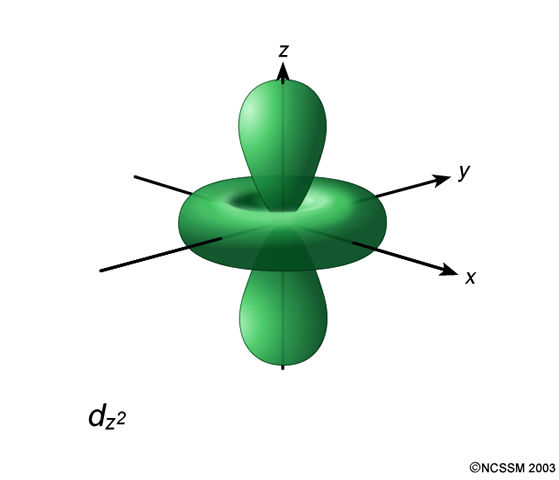
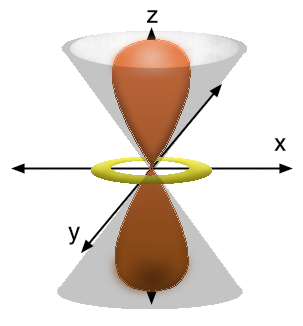
Last year, I also drew in the orbital and its node myself, so it may help you to look at this too:
For a
- The total number of nodes is
#n - 1 = 3 - 1 = bb(2)# . - The total number of radial nodes is
#n - l - 1 = 3 - 2 - 1 = bb(0)# . - The total number of angular nodes is
#l = bb(2)# .
Thus, the two conical nodes (top half and bottom half) it has are both angular, and the conical node is a kind of angular node.
The angular wave function that demonstrates this is:
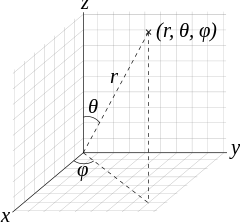
#color(green)(Y_(l)^(m_l)(theta,phi)) = Y_(2)^(0)(theta,phi) = color(green)(sqrt(5/(16pi))(3cos^2theta - 1))#
Since a node is when the wave function
#0 = 3cos^2theta - 1#
#=> cos^2theta = 1/3#
#=> theta =# #arccos(pm1/sqrt3)#
#=> color(blue)(theta ~~ 54.74^@, 125.26^@)# ,
which are the degrees of descent from the top of the
Due to how there is no
- Tilt
#54.74^@# away from the top of the#z# axis, and revolve around the#z# axis, and you have one of the angular nodes. - Tilt
#125.26^@# away from the top of the#z# axis, and revolve around the#z# axis, and you have the other angular node.
Thus, due to the two solution angles, there is an exact copy of the top half of the conical node at the bottom, giving us two angular conical nodes.

