Question #a5256
2 Answers
Nov 27, 2016
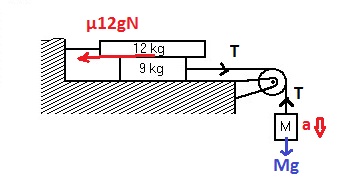
Let
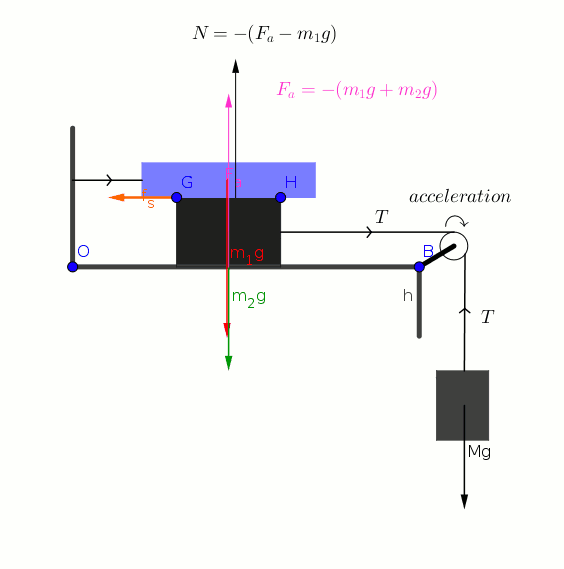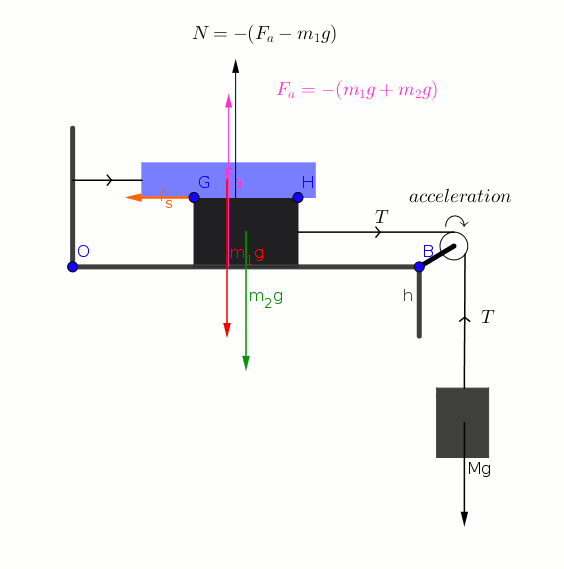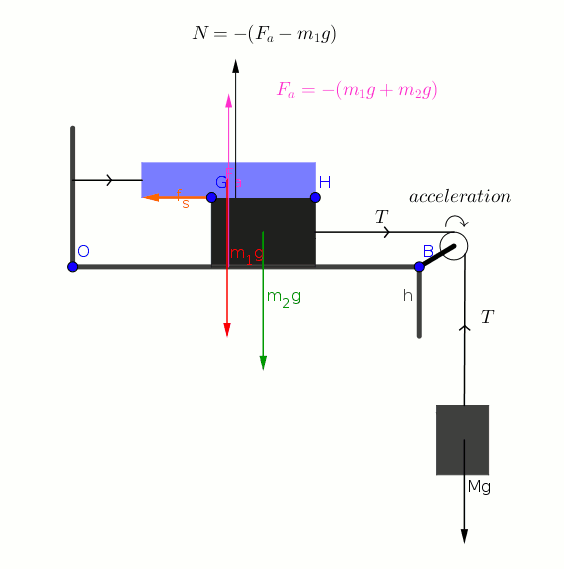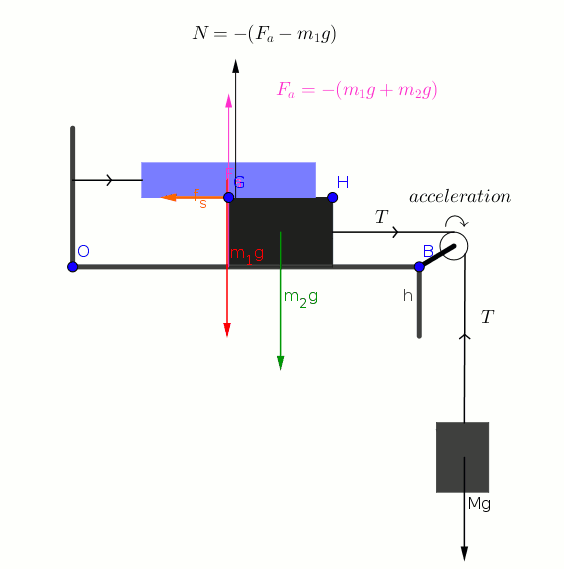
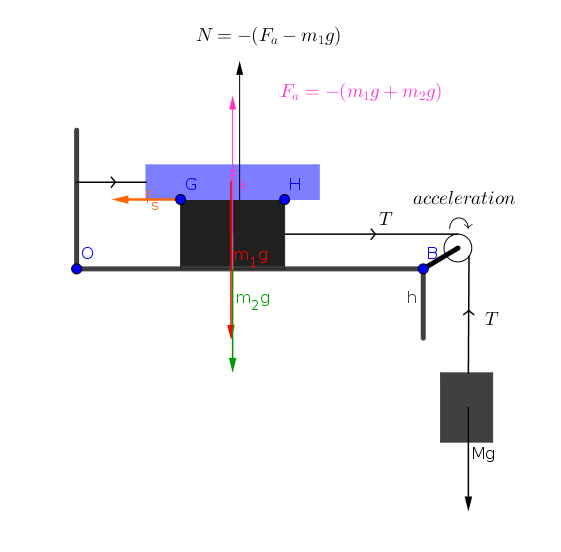
Considering the forces on 9 kg block we can write
Considering the forces on
Adding (1) and (2) we get
Apr 3, 2017
Explanation: