Question #b79c6
1 Answer
Nov 27, 2016
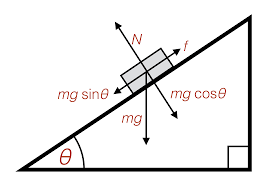
Let
Since in this case the block moves downward with constant speed the net force acting on it zero,
Here downward gravitational pull along the plane
So