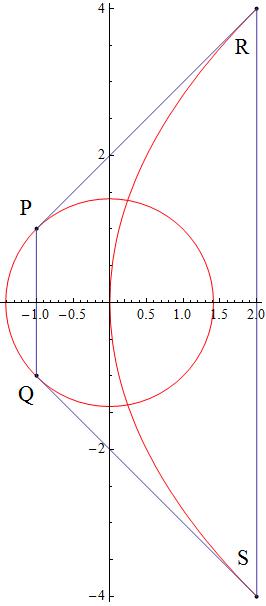
Calculate the area for the trapeze #PQRS# ? (See question)
1 Answer
Dec 10, 2016
Explanation:
Given two conics
The tangent space to those conics is
the tangency condition reads
Solving now
for
Attached a plot focusing the main elements
The area is