Find the value of?
(1) #arccos(-sqrt3/2)-arcsin(-sqrt3/2)-arccos(1/2)+arcsin(sqrt3/2)#
(2) #arcsin(-1/2)+arcsin(-sqrt3/2)#
(3) #sin(arccos(-sqrt3/2))=sin150^o#
(1)
(2)
(3)
2 Answers
(1)
(2)
(3)
Explanation:
The trigonometric ratios of standard angles are given in
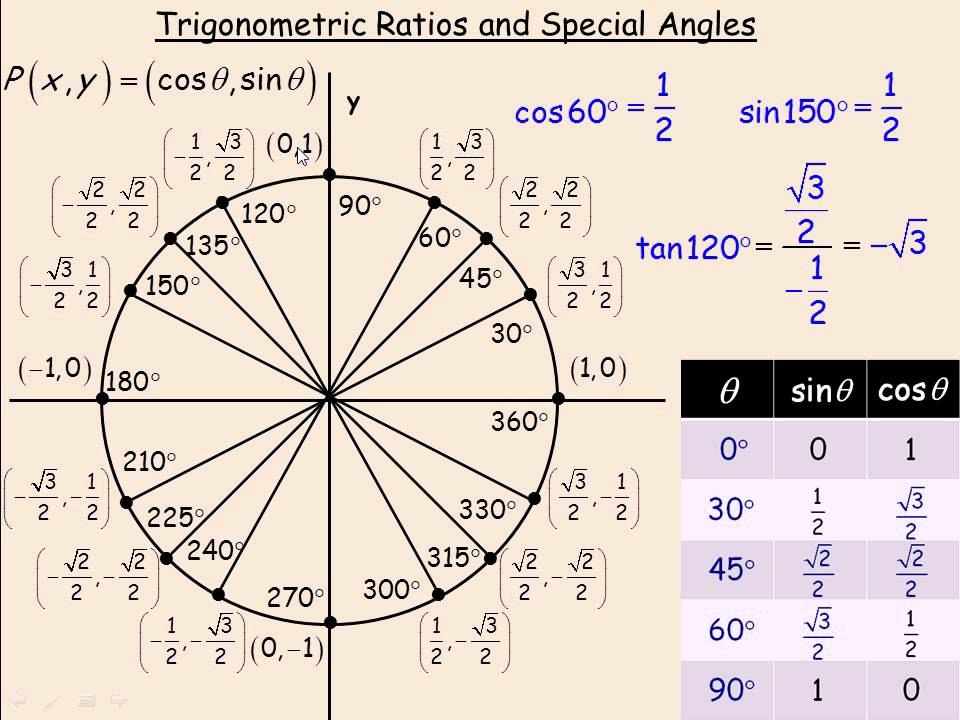
However, before we use this let us remember that range for inverse trigonometric functions are -
Considering this we solve above as follows:
(1)
=
=
(2)
=
(3)
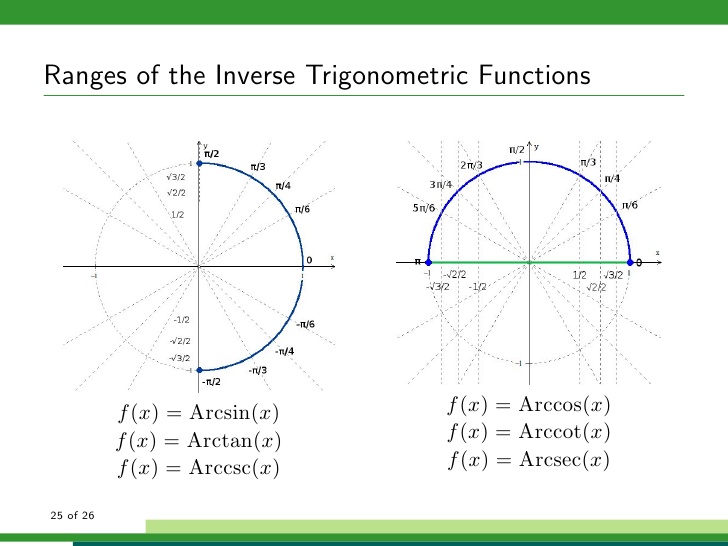
To solve this type of problem we are to remember the range of inverse trigonometric function as shown in above figure
1)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
2).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
3).

