Question #089b1
1 Answer
Kinematic equation of interest is
#v(t)=u+at# .....(1)
where#v(t)# is velocity after time#t# ,#u# is initial velocity of an object and#a# is constant acceleration experienced by it.
- Recall the expression
#"Displacement"="Velocity"xx"time"# - Observe it looks like equation of a straight line in the form
#y=mx+c# .
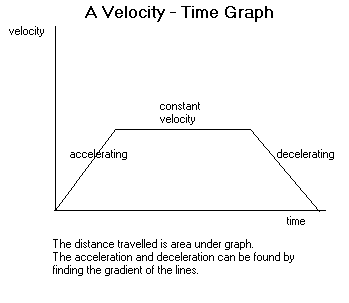
We know that velocity is rate of change of displacement, therefore equation (1) can be written as
#(ds(t))/(dt)=u+at#
#=>ds(t)=(u+at)cdot dt# .....(2)
If we integrate both sides we get
We see that LHS of the equation is total displacement, and RHS is area under the velocity-time graph from time
Equation (3) is the required expression.
One should not be surprised if one calculates integral of RHS of equation (3) from time
#s=ut+1/2at^2#
