Question

Question #93873

Answer 1

In electrical terminology, Time constant is denoted by `'tau_c'`.

Explanation:

In electrical terminology, A charge `q_o = CV` comes in the capacitor as soon as switch is closed when we take a capacitor connected to a battery of emf `V` through a switch `S` and it gets charged immediately when we close the switch.
In this case the `q-t` graph is a straight line parallel to t-axis i.e., time axis graph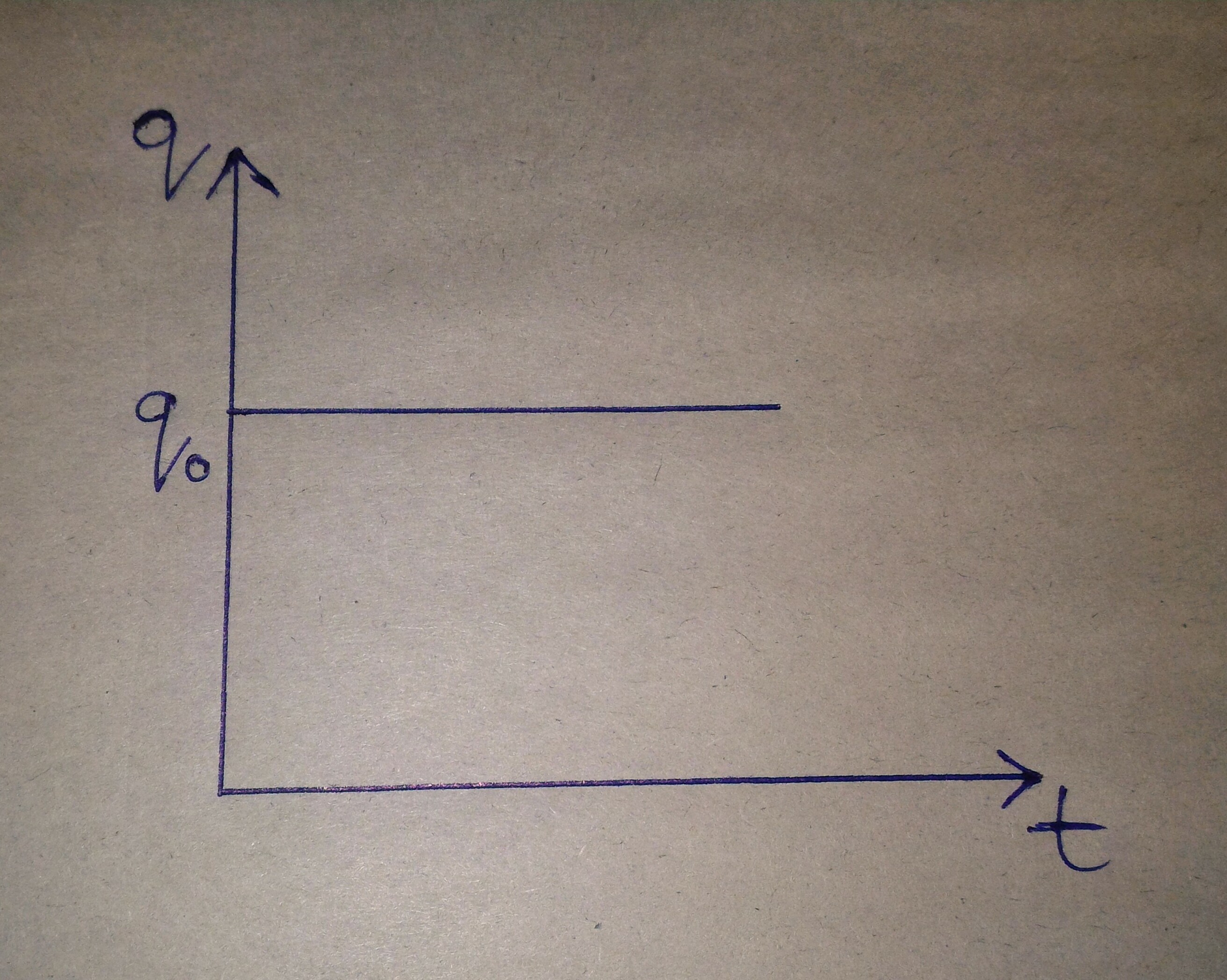
Presence of resistance in the circuit makes some time for charging, this is because resistance opposes current flow in the circuit.

Steady state charge, which is final charge is still `'q_o'` but it's acquired after a long period of time.

For this case, the `q-t` equation becomes as

`rArr` `q=q_o(1-e^(-t//tau_c))`

At `t=tau_c`,
`rArr q=q_o(1-e^(-1))=0.632q_o`
Therefore, the time constant `'tau_c'` is defined as the time in which 63.2% charging is over in a C-R circuit.

`tau_c` = time `= CR`
Its dimensional formulae:[`M^0L^0T^1`]

It is also can be defined as the time when charge reduces to 36.8% of its maximum value `q_o`, while in the discharging cases
`q=q_oe^(-1)=0.368q_o` also when at `t=tau_c`.