How do you show that in a right angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides ?

Question

7319 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-01-28T01:44:41

See explanation...

Consider this diagram:

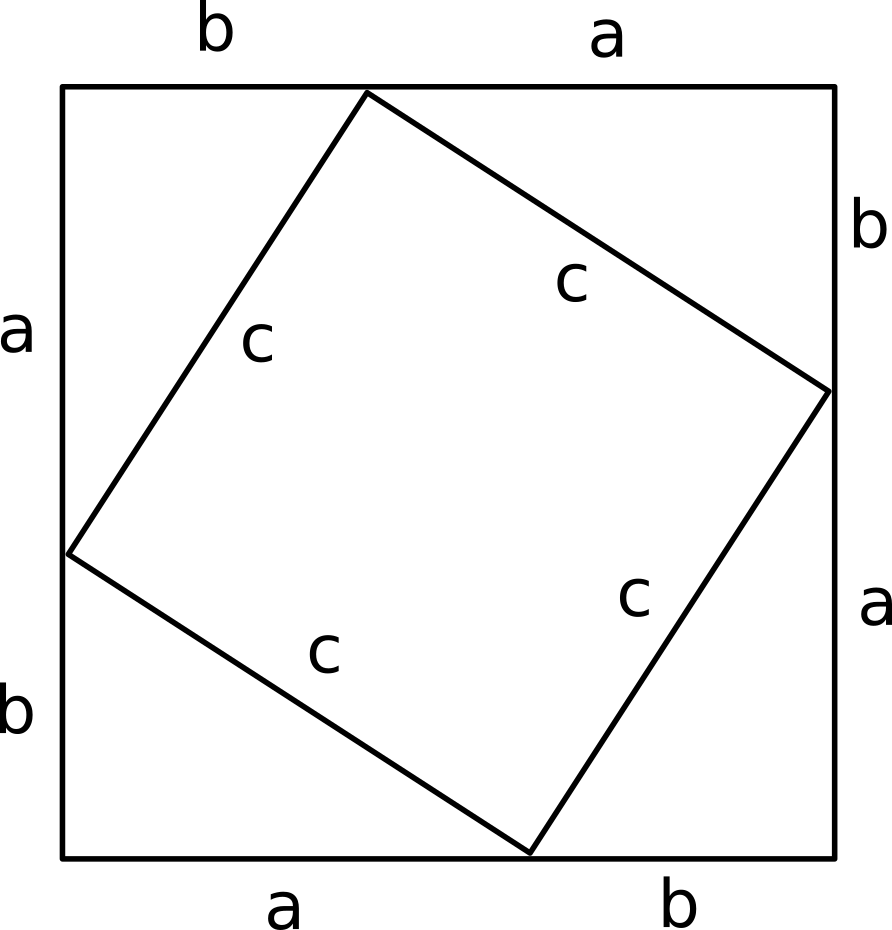
enter image source here

Each of the triangles is a right angled triangle with sides #a, b, c# and area #(ab)/2# (since it is half of an #axxb# rectangle)

The area of the large square is:

#(a+b)^2 = a^2+2ab+b^2#

The area of the smaller square plus the area of the triangles is:

#c^2+4((ab)/2) = c^2+2ab#

These two expressions must be equal. So we have:

#a^2+2ab+b^2 = c^2+2ab#

Subtracting #2ab# from both sides, we find:

#a^2+b^2=c^2#

This is Pythagoras' Theorem:

In a right angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.