Pythagorean Theorem and its Converse
Key Questions
-
-
When carpenters want to construct a guaranteed right angle, they can make a triangle with sides 3, 4, and 5 (units). By the Pythagorean Theorem, a triangle made with these side lengths is always a right triangle, because
#3^2 + 4^2 = 5^2.# -
If you want to find out the distance between two places, but you only have their coordinates (or how many blocks apart they are), the Pythagorean Theorem says the square of this distance is equal to the sum of the squared horizontal and vertical distances.
#d^2 = (x_1 - x_2)^2 + (y_1 - y_2)^2#
Say one place is at
#(2,4)# and the other is at#(3, 1)# . (These could also be latitude and longitudes, but you get the idea.) Then we square the horizontal distance:#(2 - 3)^2 = 1# and the vertical distance:
#(4 - 1)^2 = 9# add these squares,
#1 + 9 = 10# and then take the square root.
#d = sqrt10# - TV sizes are measured on the diagonal; it gives the longest screen measurement. You can figure out what size TV can fit in a space by using the Pythagorean Theorem:
#("TV size")^2 = ("space width")^2 + ("space height")^2# Note: you should also remember that TVs are usually
#16 xx 9,# so you'd likely want to measure just the width of the space, then use#"width "xx9/16# as the height of the space. -
-
Converse of Pythagoras Theorem is - If the square on one side of a triangle is equal to the sum of the squares on the other two sides, then the triangle is a right triangle.
-
We generally define the distance between two points using the Pythagorean theorem.
Consider a two dimensional Cartesian coordinate system (the same ideas can be extended to any number of dimensions. The natural way to think about the geometry of this coordinate system is using vectors.
The distance
#d(0,P)# between the origin#0# and a certain point#P# in the coordinate system is given by:#d(0,P) = sqrt(x_1^2+x_2^2),# where
#x_1# and#x_2# are the coordinates (or, thinking of the point as a vector, the lengths of it's components) of the point.Since the Cartesian system is orthogonal, the components of any vector in this space are orthogonal. Therefore, they form the two smaller sides of a right triangle, with the distance being the length of the hypothenuse of this triangle, wich can be seen as the vector joining
#0# and#P# . Using the Pythagorian theorem, we get the aforementioned distance formula.For the distances between two points
#P# and#Q# , just consider the vector obtained from the difference between vectors joining the origin to those points and aply the Pythagorian theorem to that vector, which should give you:#d(P,Q) = sqrt((x_1-y_1)^2+(x_2-y_2)^2),# where
#y_1# and#y_2# are the coordinates of the point#Q# .In more advanced Maths, it's useful to think of the distance as a more general concept, and different definitions of distance can arise, leading to the theory of metric spaces .
-
So when you have word problems, the most important thing to understand how to convert the words to mathematical models. Sometimes, it's difficult to visualize the question automatically, so it might help to underline any pieces of key information in the question, and then to draw out the problem (but don't make the drawing too complicated), and then label the numbers where needed. From there, you can apply the Pythagorean theorem and solve. Here is an example:
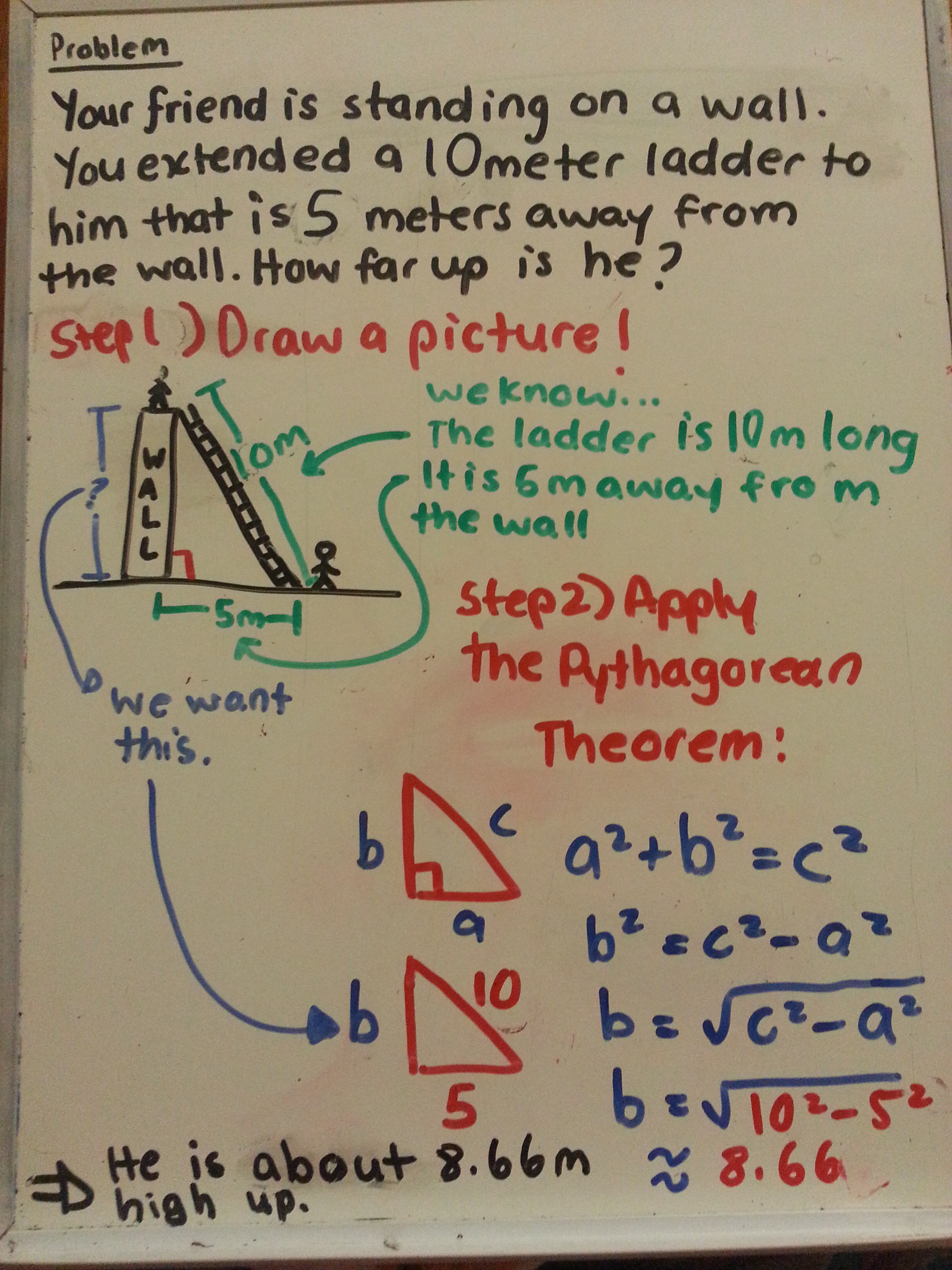
-
Pythagorean theorem:
#a^2+b^2=c^2# This only applies to right angle triangles (one of the angles is
#90^@# s)If you want to find the length of a triangle where it's A=3 B=4 C=?
you do
#3^2+4^2=?# #9+16= 25# and
#5^2=25# Therefore
C=5
you can also use it to find A or B by doing
#C^2-A^2=B^2# or#C^2-B^2=A^2#
Questions
Radicals and Geometry Connections
-
Graphs of Square Root Functions
-
Simplification of Radical Expressions
-
Addition and Subtraction of Radicals
-
Multiplication and Division of Radicals
-
Radical Equations
-
Pythagorean Theorem and its Converse
-
Distance Formula
-
Midpoint Formula
-
Measures of Central Tendency and Dispersion
-
Stem-and-Leaf Plots
-
Box-and-Whisker Plots