Question

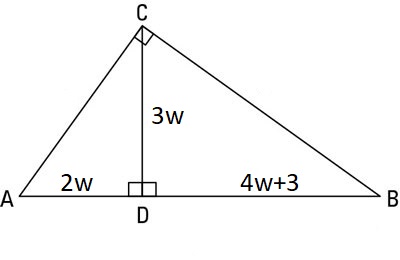
Find geometric mean and hence `w` in the following figure?

Answer 1

`w=6` and figure represents geometric mean between `12` and `27`, which is `18`.

Explanation:

You have not stated the numbers or unknowns, whose geometric mean you seek to find.

However, image enclosed by you indicates that the geometric mean between `2w` and `4w+3` is `3w`, as

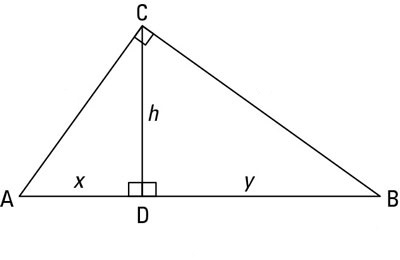
in such a figure geometric mean between `x` and `y` is `h`

or `x/h=h/y` i.e. `x xx y = h^2`. Hence, in given problem

`2wxx(4w+3)=(3w)^2`

or `8w^2+6w=9w^2`

or `w^2-6w=0`

or `w(w-6)=0` i.e. `w=0` or `w=6`

As we are dealing with a geometric figure and `w` cannot be zero (as this leads to `x=0` and `h=0`), the answer is

`w=6` and figure represents geometric mean between `12` and `27`, which is `18`.