What is the square root of #3# divided by #2# ?
1 Answer
See explanation...
Explanation:
"the square root of
-
#sqrt(3/2)" "# "the square root of:#3# divided by#2# " -
#sqrt(3)/2" "# "the square root of#3# , divided by#2# ".
A square root of a number
In either of the above interpretations of the question, the resulting number will be an irrational number - not a rational one.
Considering each in turn:
We can "simplify" the first square root
Note that if
#sqrt(3/2) = sqrt(6/4) = sqrt(6/(2^2)) = sqrt(6)/sqrt(2^2) = sqrt(6)/2#
We have:
#sqrt(3/2) = sqrt(6)/2 ~~ 1.2247#
The second expression cannot be simplified in that way:
#sqrt(3)/2#
is in simplest form.
As an approximation, we can write:
#sqrt(3)/2 ~~ 0.8660#
This particular number is important as it occurs as the height of an equilateral triangle with sides of length
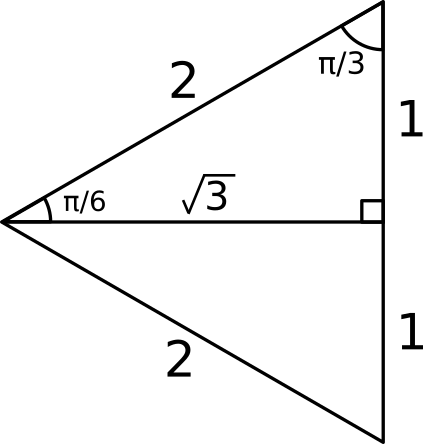
Hence we find that:
#sin(pi/3) = cos(pi/6) = sqrt(3)/2#
So when you encountered the expression "the square root of
"the square root of
#3# , divided by#2# "

