What is the total resistance of the circuit?
Circuit diagram:
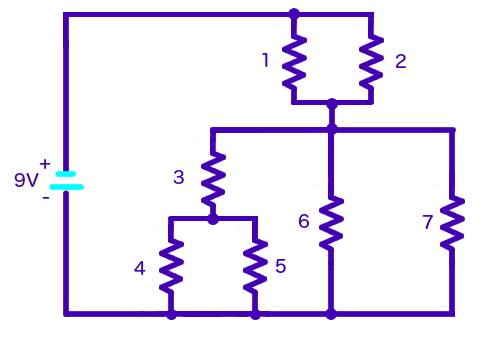
Circuit diagram:

1 Answer
The total resistance of the circuit is
Explanation:
This is a combination circuit. The best method of analysis in determining the total resistance of the circuit is to reduce it to its simplest representation, i.e. add up each of the individual resistances of each resistor. How we do this will depend on whether the resistors are connected in series or in parallel.
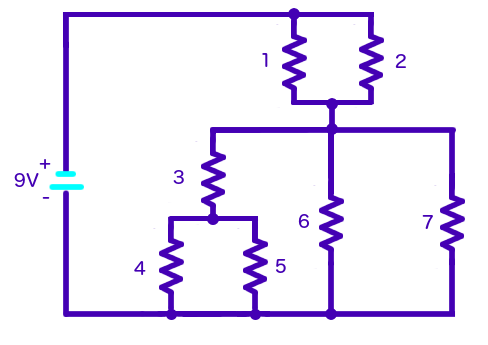
Where every resistor has resistance
#R=100# #Omega# .
Let's start from the top of the circuit, with resistors
#R_12=(1/R_1+1/R_2+...+1/R_n)^-1#
#=(1/100Omega+1/100Omega)^-1#
#=(1/50Omega)^-1#
#=50Omega#
We can now reduce
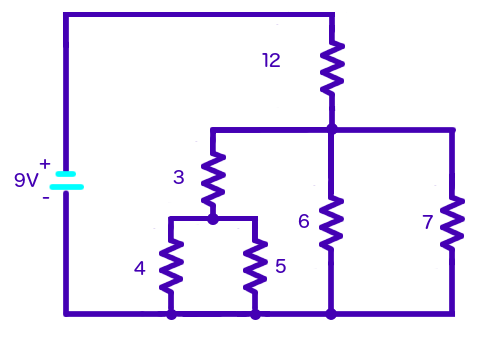
Next, let's reduce
#R_(45)=(1/R_4+1/R_5)^-1#
#=(1/100Omega+1/100Omega)^-1#
#=(1/50Omega)^-1#
#=50Omega#
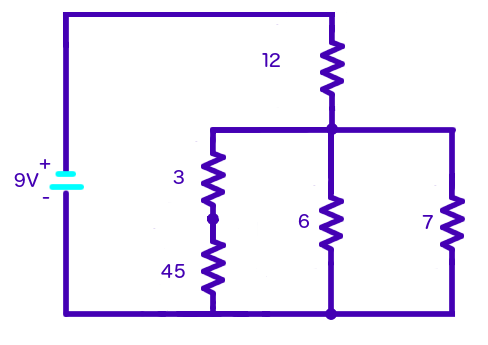
Now let's reduce
For
#R_345=R_3+R_45#
#=100Omega+50Omega#
#=150Omega#
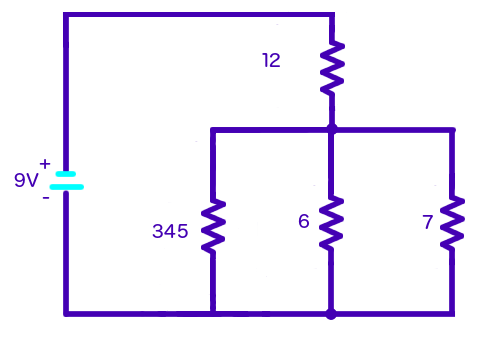
Next, let's reduce
#R_34567=(1/R_(345)+1/R_6+1/R_7)^-1#
#=(1/(150Omega)+1/(100Omega)+1/(100Omega))^-1#
#=(2/75Omega)^-1#
#=75/2Omega#
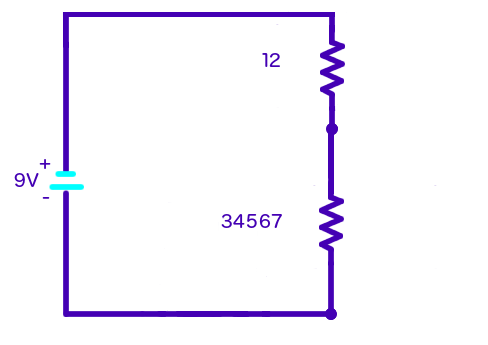
Lastly, we can add
#R_(t o t)=R_12+R_34567#
#=50Omega+75/2Omega#
#=175/2Omega#

