Answer the following questions about lithium first excited state?
#a)# How many different electron configurations can the first excited state have?
#b)# What term symbols arise in a magnetic field?
#c)# What are the #J# -coupled degeneracies?
#d)# Which term symbol represents the most stable state in the magnetic field?
#e)# Calculate the wavelength corresponding to the #""^2 P_(1//2) -> ""^2 S_(1//2)# electronic transition.
#f)# Is the transition in #(e)# allowed? How do you know?
1 Answer
Recall that the
#p# orbitals are triply degenerate. That means the first excited state of lithium will have three configurations that have the same energy.This means the following configurations are consistent with the first excited state (assume the
#1s# is doubly-occupied), where each color indicates a spot the electron could have been in:
#underbrace(ul(color(red)(uarr) color(white)(darr))" "ul(color(blue)(uarr)color(white)(darr))" "ul(color(green)(uarr)color(white)(darr)))#
#" "" "" "" """ "" "2p#
#ul(color(white)(uarr darr))#
#2s# Note that it can also be spin-down instead.
#underbrace(ul(color(red)(darr) color(white)(darr))" "ul(color(blue)(darr)color(white)(darr))" "ul(color(green)(darr)color(white)(darr)))#
#" "" "" "" """ "" "2p#
#ul(color(white)(uarr darr))#
#2s# That gives six configurations: one in each of three orbitals, two different spins, giving
#3 xx 2 = 6# .
Recall that an atomic term symbol is written as:
#bb(""^(2S+1)L_J)# where:
#S# is the total spin angular momentum and#L# is the orbital angular momentum.#M_S = sum_i m_(s,i)# is the sum of all the individual electron spins (given by#m_s# for the#i# th electron), and#S = |M_S|# . That is, if we take paired electrons, we have#S = 0# , but if they are unpaired, the sign of#M_S# is made positive after we add them all up.#M_L = sum_i m_(l,i)# is the sum of the#m_l# for each occupied orbital. We take#L = |M_L|# for the term symbol letter, and#L = 0,1,2,3, . . . # corresponds to the#S,P,D,F, . . . # terms.#J = {|L-S|, |L-S+1|, . . . , |L+S-1|, |L+S|}# , such that#J >=0# , is the total angular momentum.The reason why we have these
#J# values is that in a magnetic field, we see a phenomenon called spin-orbit coupling, in which the intrinsic angular momentum (the spin) of the electron couples with the orbital's angular momentum, lifting degeneracies and giving rise to new spin states of slightly differing energies.There would only be three possible term symbols, since there is no distinguishing between
#S# for spin-up and spin-down (#S >= 0# ).
- With one electron,
#S = |m_s| = 1/2# . Thus,#2S+1 = 2# , and we have a doublet state.- In
#p# orbitals,#l = 1# . Thus, we have only one choice of#L# :#1# .- For
#L = 1# , the range of#J# is the set#{(1+1/2), (1-1/2)}# . Thus,#J = {"1/2", "3/2"}# .This gives the following term symbols, in the order we discussed
#J# values:
#color(blue)(""^2 P_"1/2", ""^2 P_"3/2")#
(#L = 1# ,#S = 1/2# )
("doublet-p-one-half", "doublet-p-three-halves")You should also get the same term symbols for ground-state boron, which has a configuration of
#1s^2 2s^2 2p^1# . We know from the discussion above that the filled#s# orbital configurations have term symbols of just#color(blue)(""^1 S_0)# (all paired and full).
The degeneracies of each term symbol are
#2J+1# .So, the degeneracies of
#""^2 P_"1/2"# and#""^2 P_"3/2"# are#bb2# and#bb4# , respectively.All the term symbols are allowed because they correspond to valid electron configurations. Why wouldn't we be able to place one electron of arbitrary spin in one of three
#p# orbitals? (it is trivially allowed.)
From Hund's rule of maximum multiplicity for the most stable state, we first search for the maximum
#S# , then the maximum#L# .If both are identical, then the lowest
#J# for less-than-half-filled shells gives the most stable state, and vice versa for more-than half-filled shells.For exactly half-filled shells,
#M_L = 0# , so#L = 0# as well, and we would take#J = S# .Thus, since
#1 < 3# for half-filled status, the#color(blue)(""^2 P_"1/2")# is the term symbol for the most stable excited state in a magnetic field.
The
#""^2 S_"1/2"# is the state for which one electron is in an#s# orbital (#2S+1 = 2 => S = 1/2# , an#S# term#harr L = 0# ,#J = 0+1/2 = 1/2# ).So, the
#""^2 P_"1/2" -> ""^2 S_"1/2"# transition is just referring to the#2p->2s# relaxation process that transforms#1s^2 2p^1# into#1s^2 2s^1# :
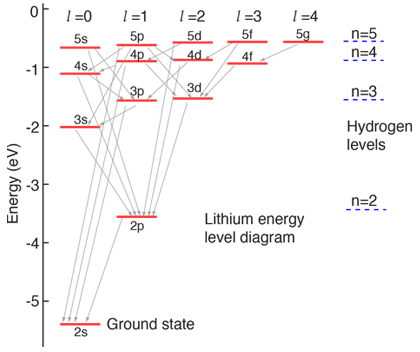
I'll let you look that up here in
#"cm"^(-1)# :http://physics.nist.gov/PhysRefData/ASD/levels_form.html
I found this table as a result (make sure you enter "Li I" in your search):
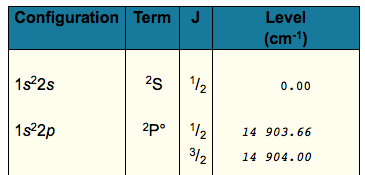
The value should turn out to be
#6708# angstroms, or#"670.8 nm"# , which is reddish light. In fact, the conversion of the#"14903.66 cm"^(-1)# is the one you want, and it gives#"670.98 nm"# .
It should be an allowed transition. Allowed transitions follow the selection rules:
#DeltaL = pm1# #DeltaS = 0# - Thus, we include
#DeltaJ = 0, pm1# .We have
#DeltaS = 0# and#DeltaL = -1# , so that is definitely within the allowed selection of transitions.Any diagonal transition on the above diagram is allowed.

