The graph of #r=1# intersects the graph of #r=2sin(theta)# when
#2sin(theta)=1#
#sin(theta)=1/2#
#theta = 2pi n + pi/6# for #n in ZZ#
Looking at the graph, we can see that those angles correspond the intersection in quadrant I and quadrant II.
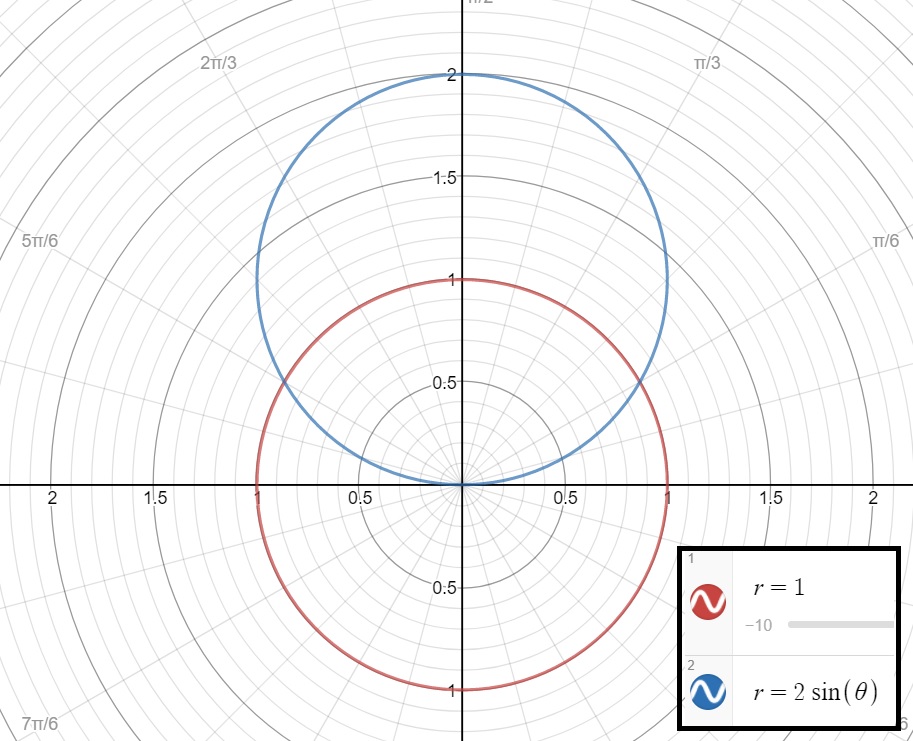
Analyzing the graph, we can develop a strategy for finding the area of the overlapping regions. For example, we could get the area of #r=1# (in red) from #theta=pi//6# to #theta=5pi//6#. Then we would need to add on both remaining slivers of #r = 2sin(theta)# (in blue). Those two slivers are identical in area, so we could add the area of #r = 2sin(theta)# between #theta=0# and #theta=pi//6#, then double it.
This gives us
#A=1/2int_(pi/6)^((5pi)/6)(1)^2d theta + 2 *1/2int_0^(pi/6) (2sin(theta))^2 d theta#
#A=[1/2 theta]_(pi/6)^((5pi)/6)-4[1/2 (θ - sin(θ) cos(θ))]_0^(pi/6)#
#A=(4pi)/12-4[1/24 (2 π - 3 sqrt(3))]~~sqrt(3)/2#

