How do you find the area between two curves using integrals?
1 Answer
First, you will take the integrals of both curves. Next, you will solve the integrals like you normally would. Finally, you will take the integral from the curve higher on the graph and subtract the integral from the lower integral.
Take for example we have two functions
Without any limits given we assume they want the area between the points that the two functions intersect so we set the two functions equal and solve.
Do to
Now that we know the bounds and the order to subtract, we can setup the integral.
And now we solve like a normal integral.
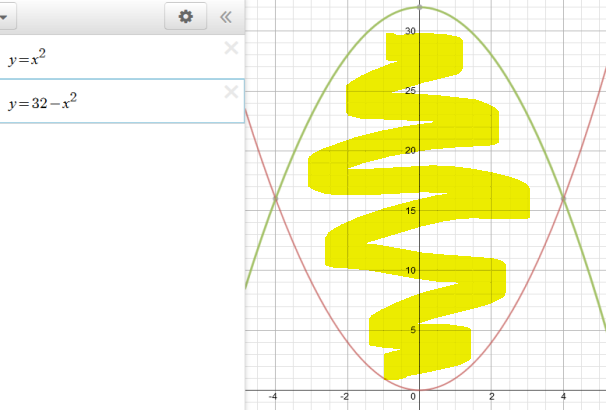
Here is a graphical example of a more complicated problems:
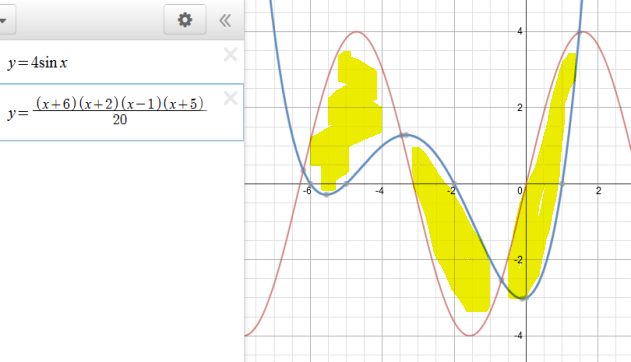
The more general form of area between curves is:
#A=int_a^b|f(x)-g(x)|dx#
because the area is always defined as a positive result.
So for this problem, you need to find all intersections between the 2 functions (we'll call red
#A=int_(-6.2)^(-3.5)[f(x)-g(x)]dx+int_(-3.5)^(-.7)[g(x)-f(x)]dx+int_(-.7)^(1.5)[f(x)-g(x)]dx#


