Calculating Areas using Integrals

Key Questions

  • How do you find the area between two curves using integrals?

    First, you will take the integrals of both curves. Next, you will solve the integrals like you normally would. Finally, you will take the integral from the curve higher on the graph and subtract the integral from the lower integral.

    Take for example we have two functions

    #f(x)=32-x^2# and #g(x)=x^2#

    Without any limits given we assume they want the area between the points that the two functions intersect so we set the two functions equal and solve.

    #32-x^2=x^2# solves to #x = 4# and #x=-4# so they become our bounds

    Do to #f(x)# is higher on the positive x-axis, we subtract #g(x)# from it.

    Now that we know the bounds and the order to subtract, we can setup the integral.

    #int_-4^4f(x)-g(x) dx= int_-4^4 32-x^2-x^2 #

    And now we solve like a normal integral.
    #F(x) = 32x-2/3x^3 +C#
    #F(4)-F(-4)=170 2/3#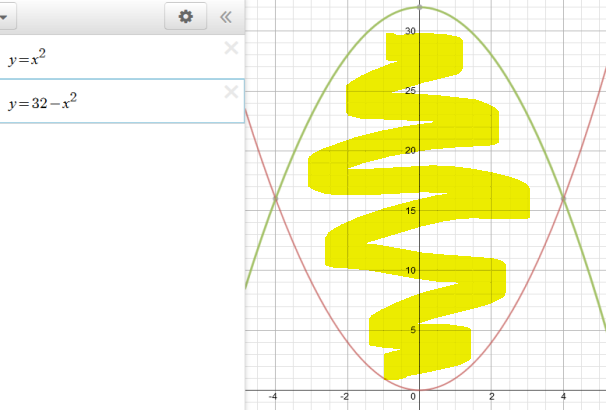

    enter image source here

    Here is a graphical example of a more complicated problems:

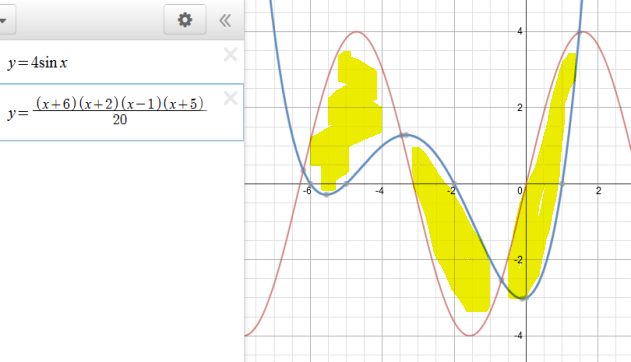
    enter image source here

    The more general form of area between curves is:

    #A=int_a^b|f(x)-g(x)|dx#
    because the area is always defined as a positive result.

    So for this problem, you need to find all intersections between the 2 functions (we'll call red #f(x)# and blue #g(x)# and you can see that there are 4 at approximately: #-6.2#, #-3.5#, #-.7#, #1.5#. So, we look at which function is greater on those intervals for the full integral:

    #A=int_(-6.2)^(-3.5)[f(x)-g(x)]dx+int_(-3.5)^(-.7)[g(x)-f(x)]dx+int_(-.7)^(1.5)[f(x)-g(x)]dx#

    Michael B. · 1 · Sep 3 2014
  • How do you find the area under a curve using integrals?

    Finding the area under a curve is easy use and integral is pretty simple. First you take the indefinite that solve it using your higher and lower bounds. Lastly you subtract the answer from the higher bound from the lower bound.

    For example, lets take the function,

    #f(x) = x#

    and we want to know the area under it between the points where
    #x=0# and #x=5#.

    First you set up your integral #int_0^5 x dx#.

    Next you find the indefinite integral.

    #int xdx = 1/2*x^2+C#

    Now you plugin the 5 and the 0 and solve

    #(1/2*5^2+C)-(1/2*0^2+C)=12.5#

    Because this example forms a triangle, we can check the answer with the equation for the area

    #A=1/2*5*5=12.5#

    Michael B. · · Sep 3 2014

Questions

Using Integrals to Find Areas and Volumes